6 способов посчитать проценты от суммы с калькулятором и без

Примеры с процентами

Пример 1

Найдите 60% от числа 250.

Решение:

Число 250 будет нашим целым, то есть это 100%. Нам нужно найти 60%. Отношение 60 к 100 будет равно отношению неизвестного числа к 250:

60/100 = Х/250

Произведение крайних будет равно произведению внутренних, то есть 100 умножить на Х равно 250 умножить на 60:

250 х 60 = 100 х Х

Решаем простое уравнение и получаем 150.

Ответ: 150

Пример 2

Найдите число, если его 40% равняется 100.

Решение:

Строим пропорцию:

40/100 = 100/X

Решаем по алгоритму из первого примера, только здесь неизвестен один из крайних элементов.

100 х 100 = 40 х Х

Х = 250

Ответ: 250

Еще больше примеров — в детской школе Skysmart. Ученики решают задачки в интерактивном формате с мгновенной автоматической проверкой, отслеживают прогресс в личном кабинете и чувствуют себя увереннее на школьных контрольных.

Запишите ребенка на бесплатный вводный урок: покажем, как у нас все устроено и вдохновим на учебу!

Что такое процент?

Процент это сотая часть чего-либо

Неважно чего, это может быть:

• Разделение общественных мнений в опросах: 35 % людей высказались за изменение закона.
• Выделение элементов в химических реакциях: в результате окисления 40% бора из твердого состояния перешли в газообразное.
• Показатели экономики: ВВП страны увеличилось на 6 % за год и т.д.

В математике проценты чаще всего используют в задачах для того, чтобы усложнить условие.

Единственная вещь в математике, которую нельзя измерять в процентах это вероятности. Но при этом ученики регулярно допускают ошибки и ответы в задачах на теорию вероятности пишут в процентах. Запомните, так делать нельзя.

Сложные проценты

РешитьСложная процентная ставка наращенияm=12m=4S=P·(1+im​)m·nсмешанным методомn

Современная стоимость Р величины S находится в случае сложной процентной ставки по формуле:
P=S(1+i)n​

Примеры задач на сложные проценты

1. Какой величины достигнет долг, равный P = 1 млн.руб., через n = 5 лет при росте по сложной ставке i = 15,5% годовых, если проценты начисляются раз в год, ежемесячно, поквартально и два раза в год?
   1) Сложные проценты начисляются раз в год:
   2) Сложные проценты начисляются два раза в год:
   S=1 000 000·(1+0,1552​)2·5 = 2 109 467,26 руб.
   3) Сложные проценты начисляются 4 раза в год (поквартально):
   S=1 000 000·(1+0,1554​)4·5 = 2 139 049,01 руб.
   4) Сложные проценты начисляются ежемесячно (12 раз в год):
   S=1 000 000·(1+0,15512​)12·5 = 2 159 847,20 руб.
2. Через n = 5 лет предприятию будет выплачена сумма S = 1 млн.руб. Определить ее современную стоимость при условии, что применяется ставка сложных процентов i = 10% годовых.
   P=S(1+i)n​
   P=1 000 000(1+0,1)5​ = 620 921,32 руб.
   Если проценты начислялись ежеквартально.
   P=S(1+im​)m·n​
   P=1 000 000(1+0,14​)4·5​ = 610 270,94 руб.
3. Определить современную стоимость S = 20 тыс.руб., которые должны быть выплачены через четыре года (n = 4). В течение этого периода на первоначальную сумму начислялись сложные проценты по i = 8 %годовых: а)ежегодно; б)ежеквартально.
   P=S(1+i)n​
   P=20 000(1+0,08)4​ = 14 568,92 руб.
   Если проценты начислялись ежеквартально.
   P=S(1+im​)m·n​
   P=20 000(1+0,084​)4·4​ = 14 570 руб.
4. За взятые в долг деньги под сложную процентную ставку i=35% годовых должник обязан уплатить кредитору 30 тыс. руб. 1 июля 1997 г. Какую сумму необходимо уплатить должнику, если он вернет долг: а) 1 января 1997 г.; б) 1 января 1998 г.; в) 1 июля 1999 г.?
   Количество дней в 1997 году: T=365.
   а) 1 января 1997 г.;
   Эта дата ранее 1 июля 1997 г., поэтому речь идет о поиске P (S=30000). Количество дней между 1 января 1997 г. и 1 июля 1997 г. составляет d=181 дн..
   б) 1 января 1998 г.;
   Эта дата позже 1 июля 1997 г., поэтому находим S (P=30000). d1=01.07.1997 и d2=01.01.1998.
   в) 1 июля 1999 г.Количество лет между 1 июля 1997 г. и 1 июля 1999 г. составляет n=2 года.
   S=P·(1+i)n=30000·(1+0.35)2 = 54 675 руб.

Безрисковая процентная ставка

Так принято называть
процентную ставку по финансовому
инструменту с относительно низким
уровнем риска. Например, ставку купонного
дохода по государственным облигациям,
которые считаются наиболее надёжными
ценными бумагами. Или же, безрисковой
можно считать ставку по банковскому
депозиту, ведь все вклады физических
лиц подпадают под программу государственного
страхования**

В инвестициях риск есть
всегда и чем больше их потенциальная
доходность, тем выше уровень риска.
Именно поэтому доходность финансовых
инструментов с безрисковой процентной
ставкой находится на минимальном уровне
(зачастую она едва превышает уровень
инфляции).

Инвестируя даже в самые
надёжные государственные облигации и
банковские вклады можно столкнуться с
такими рисками как:

• Неблагоприятное
  изменение процентной ставки;
• Политические перемены;
• Риск дефолта;
• Другие непрогнозируемые
  обязательства.

Для чего введено понятие
безрисковой процентной ставки? Дело в
том, что всё в этом мире относительно и
сильно зависит от той конкретной
отправной точки, с позиций которой
ведётся оценка. Так и в данном случае,
безрисковая ставка служит отправной
точкой для расчёта и оценки процентных
ставок по другим финансовым инструментам.

Эффективность того или
иного вложения можно оценить по тому
количеству пунктов, на которое процентная
доходность по нему превышает безрисковый
уровень. Например, процентная ставка
по корпоративным облигациям в 14% годовых
смотрится весьма привлекательно
относительно 8% которые дают по банковским
депозитам.

Безрисковая процентная
ставка может быть двух основных видов:

1. Нарицательная;
2. Реальная.

Под нарицательной
понимается процентная ставка по
финансовым инструментам с максимальным
уровнем надёжности и минимальным уровнем
риска (как в рассмотренных выше примерах
с государственными облигациями и
банковскими вкладами). А реальной,
называют нарицательную безрисковую
ставку за вычетом текущего уровня
инфляции.

Оценивая привлекательность
инвестиционного проекта смотрят именно
на реальную безрисковую процентную
ставку, которая в данном случае выступает
в качестве той премии за риск, которую
получит инвестор в результате удачной
реализации рассматриваемого проекта.

** До суммы вклада не
превышающей 1400000 рублей.

Как найти базовую сумму исходя из ее процента

В некоторых случаях нам может быть известно какое-либо число и процент, которое оно составляет от базового числа. Нам необходимо определить значение. Например, нам может быть дана сумма 67, которое составляет 23% от базового числа. Каково же само базовое число?

Для решения этой задачи нам необходимо 67 разделить на 23 и умножить на 100. Формула вычисления процента выглядит следующим образом:

67 / B * 100 = A

Подставляем значения:

67 / 23 * 100 = 293, 31 (десятые после запятой можем округлить)

Проверяем полученный результат с помощью формулы из первого способа:

293, 31 / 100 * 23 = 67

Всё сошлось.

Немного экономики

Сегодня довольно популярный вопрос – оформление кредита на определенный срок. Но как выбрать выгодный заем, чтобы не переплачивать? Во-первых, нужно посмотреть процентную ставку. Желательно, чтобы этот показатель был как можно ниже. Затем следует применить формулу расчета процентов по кредиту.

Как правило, на размер переплаты влияет сумма долга, процентная ставка и способ погашения. Различают аннуитетные и дифференцированные платежи. В первом случае кредит погашается равными долями каждый месяц. Тут же сумма, которая перекрывает основной заем, растет, а стоимость процентов постепенно уменьшается. Во втором случае кредитозаемщик выплачивает постоянные суммы на погашение займа, к которым прибавляются проценты на остаток основного долга. Ежемесячно общая сумма выплат будет уменьшаться.

Теперь нужно рассмотреть оба способа погашения кредита. Так, при аннуитетном варианте сумма переплаты будет выше, а при дифференциальном – сумма первых платежей. Естественно, условия кредита одинаковы для обоих случаев.

Как в Эксель посчитать процент от числа

Простой расчет – получаем процент от одного числа. В ячейку A1 введем число, например 70. В ячейку B1 введем второе число, например 38. Вопрос, какой процент составляет число 38 от числа 70? Установим процентный формат для ячейки C1, в этой же ячейке нужно прописать формулу:

Формула вводится после знака = и отображается в строке формул. В ячейке A3 отобразится результат.

Усложняем задачу. Нужно рассчитать 5% от некоторых чисел. Пусть это будет 5 чисел в таблице. Введем в ячейку C1 значение 5%. В ячейку B1 введем формулу:

И выполним автозаполнение. Таким образом, в столбце B у нас будут значения соответствующие 5 процентам от числа в столбце A.

Знаки $ фиксируют ячейку C1. То есть, изменив значение с 5% до 8% (или иное) значения в столбце B пересчитаются автоматически.

Другой пример расчета процентов Excel

Итак, нам необходимо определить, какой процент составляют реализованные товары от общего количества продуктов на складе.

Для этого требуется выполнить следующие действия:

• В ячейку D2 вписать формулу =С2/D2 (количество проданных товаров/общее число продуктов) и нажать клавишу Enter.
• Чтобы не тратить время, рекомендуется воспользоваться функцией автозаполнения– растянуть формулу вниз настолько, насколько необходимо.
• Выделить все заполненные ячейки в столбце D и установить процентный формат.
• Оценить результат:

Выбрать процентный формат для ячейки можно четырьмя способами:

Выделив необходимые ячейки, перейти в контекстное меню правой клавишей мыши

Обратите внимание, что в этом случае есть возможность самостоятельно настроить количество знаков после точки.
Воспользоваться комбинацией клавиш Ctrl+Shift+5.
Выбрать формат во вкладке «главная» на панели задач.
Вписать число со знаком % — программа самостоятельно подберет нужный формат.. Иногда возникает обратная ситуация – необходимо определить, сколько составляет процент проданных товаров в числовом значении

Для этого достаточно выделить ячейку, для которой требуется получить результат, и умножить процент на целое число

Иногда возникает обратная ситуация – необходимо определить, сколько составляет процент проданных товаров в числовом значении. Для этого достаточно выделить ячейку, для которой требуется получить результат, и умножить процент на целое число.

Определение процентного соотношения чисел

Вычислить процентное соотношение чисел в Excel очень просто! Необходимость выполнения этой задачи возникает достаточно часто – например, в случае, когда нужно оценить изменение уровня продаж за прошлый и текущий период.

Чтобы понять, насколько увеличились продажи в сентябре, необходимо сделать следующее:

• Задать в ячейке D2 формулу =(С2-B2)/B2 и нажать клавишу Enter.
• Протянуть D2 вниз на нужное количество строк.
• Выделить полученные данные и перевести в процентный формат любым удобным способом.

Положительное значение в столбце D показывает прибыль, отрицательное – соответственно, убыток.

Чтобы наглядно оценить результаты деятельности, можно сделать диаграмму. Для этого надо выделить столбец с процентами и выбрать тип диаграммы во вкладке «вставка».

Разница процентов в Экселе, как вычесть процент

Приведу другой пример, аналогичный предыдущему. Иногда нам нужно рассчитать разницу в процентах. Например, в 2017 году мы продали товаров на 2902345 рублей, а в 2018 году на 2589632 рублей.

Сделаем заготовку. И произведем расчеты.

В ячейке C2 введем формулу:

Данная форма показывает разницу между суммами в процентах. В данном примере мы продали товар в 2018 году на сумму меньшую, чем в 2017 году на 10,77%. О меньшей сумме свидетельствует знак минус. Если знак минус отсутствует, значит мы продали на большую сумму.

Если у вас много данных советую закрепить область в Excel.

Как посчитать процент выполнения плана в Excel

Процент выполнения плана в целом считается так же, как я описывал выше. Но давайте разберемся на более конкретном примере. А именно на плане учета рабочего времени.

Пример будет простой. Сотрудник получает заработную плату 10000 рублей в месяц в зависимости от процента отработанных дней в месяце. А так же сотрудник получает премию в размере 8000 в зависимости от выполнения плана продаж.

Сделаем таблицу для расчетов.

Далее все довольно просто. Что бы рассчитать процент выполнение нужно факт разделить на план.

Соответствующий процент умножить на ставку, а затем суммировать. Конечна сумма будет оплатой труда сотрудника за месяц.

Пример сложного процента на банковском депозите

Удобно и выгодно, когда ваши деньги одномоментно задействованы в разных инструментах. Сразу рекомендую не только у менеджера устно, но и в письменном договоре детально изучить — какой именно процент используется и какие есть нюансы по нему. На некоторых банковских сайтах или в мобильных приложениях есть калькулятор сложных процентов с капитализацией и пополнением. Показываю, как работает эта формула.

1. Первоначальный вклад составил 100 тыс. рублей на 1 год с правом пополнения без ограничения суммы под 5% годовых.
2. Во втором полугодии вы добавили к вкладу еще 100 тыс. рублей.
3. За первую половину вы заработали (100000/100*5%) / 2=2500. Во втором полугодии получили (200000/100*5%) / 2 = 5000. Итого прибыль за год 7500.
4. Далее вы можете забрать свои 7500 или добавить их к 200 тыс. или увеличить вклад еще на определенную сумму.

Наиболее выгодно так работать с проверенными инструментами, поэтапно повышая сумму вклада и внося все данные в excel, чтобы не заблудиться.

 
Как правило, разница на доходе с правом неограниченного пополнения и на обычном способе не превышает 0,5-1% в год, а иногда и вовсе отсутствует.

Ради справедливости нужно рассмотреть и правило, как работает формула расчета простых процентов по кредиту, поскольку ее часто применяют в работе. Простой процент начисляется так: сумма кредита умножается на процентную ставку и поделенная на 365 дней. Для примера: у вас кредит на 100 тыс. рублей под 10% годовых. Если предложен дифференцированный способ, то ежемесячно вам будет начисляться 1000 рублей непосредственно за пользование средствами.

Оплачивая их, через определенный срок можно приступить к погашению самого «тела». Многие банки предлагают аннуитетный платеж, работающий по формуле сложного процента. Это означает, что вы будете оплачивать кредит плюс-минус равными долями. 1000 рублей в месяц за сам кредит и, например, 1000 рублей за само тело. Таким образом, уже на второй месяц проценты будут начисляться на 99 тыс. остатка и с каждым месяцем и платеж по процентам, и выплаты по кредиту будут уменьшаться.

Обратите внимание: сложные проценты по кредиту предлагаются на средних и высоких суммах, в частности, когда оформляете ипотеку или покупаете по договору автомобиль из салона. Хотя есть и аналогичные предложения среди кредитных карт, например, карта Халва, где выплаты подразумеваются равными долями за определенный период и иногда вовсе с минимальными процентами

Узнав способ начисления процента в рабочем инструменте, возможность вносить дополнительно средства или погашать кредит досрочно, важно обратить внимание еще на один аспект — ставку дисконтирования. Это величина, применяемая для пересчета грядущих денежных потоков в общую величину актуальной стоимости. С математической точки зрения, это формула, обратная сложному проценту

С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля

С математической точки зрения, это формула, обратная сложному проценту. С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля.

 
Учитывайте правило: ставка дисконтирования должна быть выше предложенной доходности.

В итоге подчеркну: сложные проценты в финансовых инструментах только на первый взгляд выглядят сложными, но, если разобраться в их сути, никаких камней преткновения не возникнет, а еще более — вы сможете получить существенную выгоду. Всем желаю только выгодных начислений для инвестиций и минимальных для кредита, если же вы все же решились его оформить.

Профессиональный инвестор с опытом работы 5 лет с разными финансовыми инструментами, ведет свой блог и консультирует вкладчиков. Собственные эффективные методики и информационное сопровождение инвестиций.

Как сделать диаграмму с процентами

Первый вариант: сделать столбец в таблице с данными. Затем использовать эти данные для построения диаграммы. Выделяем ячейки с процентами и копируем – нажимаем «Вставка» – выбираем тип диаграммы – ОК.

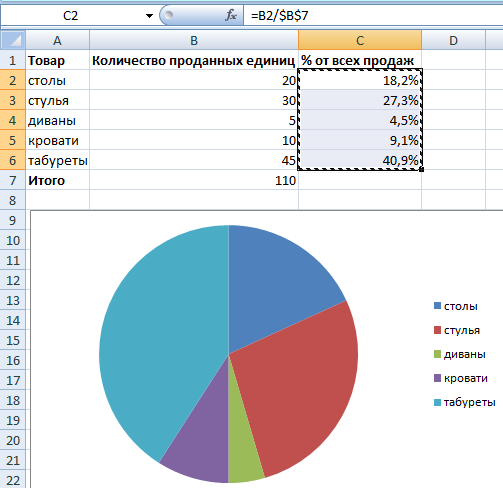
Второй вариант: задать формат подписей данных в виде доли. В мае – 22 рабочих смены. Нужно посчитать в процентах: сколько отработал каждый рабочий. Составляем таблицу, где первый столбец – количество рабочих дней, второй – число выходных.

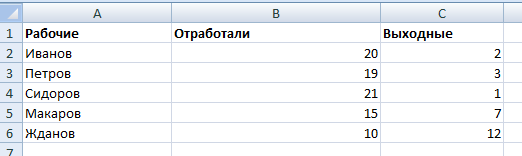
Делаем круговую диаграмму. Выделяем данные в двух столбцах – копируем – «Вставка» – диаграмма – тип – ОК. Затем вставляем данные. Щелкаем по ним правой кнопкой мыши – «Формат подписей данных».

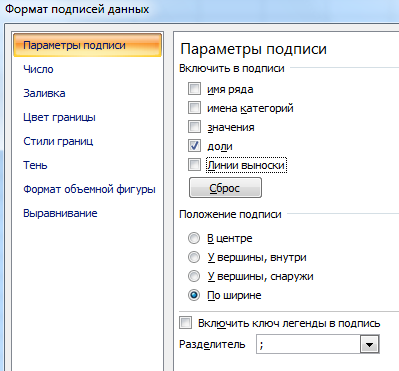
Выбираем «Доли». На вкладке «Число» – процентный формат. Получается так:

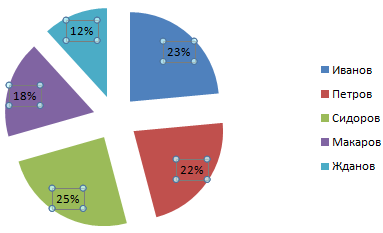
Мы на этом остановимся. А Вы можете редактировать на свой вкус: изменить цвет, вид диаграммы, сделать подчеркивания и т.п.

Похожие термины:

• процентные платежи, исчисленные до вычета взимаемых налогов.

• обозначение котировки облигаций, означающее, что покупатель получит и стоимость облигации, и проценты по ней.

• 1) проценты, которые банк должен выплатить вкладчикам по депозитам за определенный период времени; 2) проценты, уплачиваемых заемщиками банку за предоставление кредита; 3) часть процентов по облига

• процентные платежи после вычета налогов.

• форма расчета дохода на процент, основанная на арифметической прогрессии. С помощью простых процентов рассчитывается доход на вклад при сроке его хранения меньше года: d=Snj/ 360, где d — доход: S — исход

• проценты за незаконное пользование чужими денежными средствами. Определяются установленными Банком России средними ставками банковского процента по вкладам физических лиц, за соответствующий

• проценты, предусмотренные на сумму денежного обязательства за период пользования денежными средствами, подлежащие начислению. Размер процентов определяется действовавшей в соответствующие пер

• кредитор по умолчанию имеет право на получение с должника процентов на сумму долга за период, пока тот пользуется денежными средствами. Если они этого не сделают, то он будет равен ставке рефинанс

• прибыль от банковского предпринимательства за вычетом взаимных платежей из прибыли.

• процент по облигации, образовавшийся с момента последней выплаты по ней. При покупке такой облигации Н.п. включается в ее цену и возвращается затем обладателю при очередной выплате процентов.

• плата, осуществляемая заемщиком кредитору за пользование кредитом.

• размер ставки, рассчитанный с учетом продолжительности года в 365 дней, а не 360 дней, как принято в банковской практике.

• ставка рефинансирования на день уплаты заемщиком суммы долга или его соответствующей части, существующая в месте жительства заимодавца (месте нахождения юридического лица), применяемая в случае

• долговые обязательства, по которым должник выплачивает кредитору процент за предоставленную ссуду.

• процент приведения капиталовложений на будущий период времени к их стоимости в текущем периоде, вычисленный с учетом риска капиталовложений.

• процент, взимаемый банком с суммы векселя при покупке его лондонским банком и вексельным маклером до наступления срока платежа.

• плата, взимаемая банками за авансирование денег путем учета векселей, ценных бумаг, купонов, акций и облигаций, а также других долговых обязательств до наступления сроков оплаты по ним.

• ставка процента в условиях его начисления за периоды меньше года. Годовая ставка процента рассчитывается по формуле: [(1 + n/m)m -I], где n — номинальная годовая ставка, m — число периодов начисления проце

• см. ПРОЦЕНТНЫЙ АРБИТРАЖ С ЦЕЛЬЮ СТРАХОВАНИЯ

• свидетельство или купон на получение дивиденда.

Простые проценты

Чтобы понять суть явления, разберёмся с его определением, рассмотрим пример и ознакомимся с формулой, по которой простые проценты высчитываются. Об этом ниже.

Общая суть

Если говорить простыми словами, ПП – зачисление платежа в награду за хранение вклада на счёте в банке за весь период действия реквизита.

Важно! ПП можно получить только после завершения действия депозитного соглашения. Они определяются годовой ставкой по процентам

Примечание 1. Когда договор в автоматическом режиме пролонгируется на очередной период, вознаграждение за предыдущий не прибавляется к телу депозита.

Пример 1. Клиент положил на счёт в кредитно-финансовой организации сумму в 50 000 российских рублей под 7% годовых. Срок – один год. Когда действие договора подошло к концу, прибыль составила: 50 000 * 0,07 = 3 500 руб. Если соглашение автоматически продлено, для следующего периода прибыль снова будет равна 3 500. Итого через два года в банке получится забрать 50 000 + 3 500 * 2 = 57 000.

Формула

Для понимания данной схемы начисления прибыли в целом нужно запомнить формулу. Для простых процентов она такая: K = D * p.

Что означают элементы:

• K – это суммарный итог по прибыли;
• D – депозитное тело;
• p – ставка по процентам за год.

Примечание 2. Учитывайте, что для расчётов нужно годовой процент делить на 100. Т.е. 7% = 0,07.

Если речь идёт о вкладе, который создан на срок менее года, p следует делить на количество месяцев в году (12) и умножать потом на количество месяцев, на протяжении которых деньги хранились на счёте в банке.

Пример 2. Период действия депозита – 3 месяца, ставка по процентам – 10%, сумма – 50 000 руб. Тогда: 50 000 * (0,1 / 12 * 3) = 1 250 руб. Такую сумму Вы получите в качестве прибыли за время активности договора.

0,1 – это 10% ставки, 3 – срок соглашения (количество месяцев).

Несмотря на все эти цифры и буквы, процедура расчётов совсем несложная. Главное – быть внимательными и подставлять нужные значения, а также корректно производить все вычисления.

Всё сказанное говорит о том, что простая схема в теории – для тех пользователей банковского сервиса, кто имеет необходимость в относительно краткосрочных вкладах. Продолжительное содержание депозита с простым начислением процентов не слишком выгодно. Хотя, как обычно, всегда есть свои весомые нюансы для каждого отдельного случая.

Сравнительная таблица

Основа для сравнения	Простой интерес	Сложный процент
Имея в виду	Простые проценты относятся к процентам, которые рассчитываются как процент от основной суммы.	Сложный процент относится к проценту, который рассчитывается как процент от основной суммы и начисленных процентов.
Вернуть	Меньше	Сравнительно высокий
принципал	постоянная	Продолжает меняться в течение всего периода заимствования.
рост	Остается однородным	Быстро увеличивается
Проценты начисляются на	принципал	Основной + накопленный интерес
формула	Простой интерес = P * r * n	Сложный процент = P * (1 + r) ^ nk

Создаем диаграмму в диаграмме Excel

Приступим к выполнению каждого действия, производимого при построении комбинированных графиков, гистограмм или других типов диаграмм

Важно разобраться абсолютно с каждым шагом, ведь от этого зависит правильность отображения значений и удобство дальнейшей настройки

1. Вставка диаграммы производится уже после того, как все значения выделены, а значит, это нужно сделать прямо сейчас, зажав левую кнопку мыши и проведя курсором по всем блокам. Захватите и названия столбцов, чтобы они соответствовали названиям осей.

Когда все ячейки будут выделены, перейдите на вкладку «Вставка».

В разделе «Диаграммы» определитесь с тем, каким будет первый график.

Разверните весь список, посмотрите доступные варианты и нажмите по подходящему.

Диаграмма сразу же поместится в таблицу, а вы сможете заняться изменением ее размера и подбором подходящего расположения.

Разберемся с теми значениями, для которых и нужно создать график, отличающийся от первого. Изначально может сложиться такая ситуация, что из-за большой разницы в диапазоне значений его ось не будет видна в диаграмме, поэтому нужно ее настроить.

1. Кликните по ряду правой кнопкой мыши и в контекстном меню выберите пункт «Изменить тип диаграммы для ряда».

Отметьте галочкой пункт «Вспомогательная ось», которая и позволит нормализовать отображение.

Окно настройки можно не закрывать, поскольку оно еще пригодится, а вот изменения доступны для просмотра прямо вверху.

Теперь остается только изменить тип диаграммы, для чего разверните выпадающее меню «Тип диаграммы».

В таком же списке, как отображается на вкладке «Вкладка», найдите подходящую диаграмму и примените ее.

Вернитесь к таблице для проверки внесенных в диаграмму изменений.

Если же сводок значений больше двух, проделайте ту же операцию с другими рядами, предварительно подключив для них вспомогательные оси в случае проблем с правильностью отображения данных. Не бойтесь использовать совершенно разные виды диаграмм, чтобы каждый ряд выделялся и все сведения были понятны с первого взгляда.

Дополнительные настройки

В завершение пробежимся по основным настройкам, которые можно изменить в созданной комбинированной диаграмме. Например, вас не устраивает диапазон чисел, отображающийся по одной из осей. Для редактирования дважды нажмите по ней.

В появившемся окне ознакомьтесь с настройками вкладки «Параметры оси». Помимо визуальных изменений внизу есть и выбор разбежности в значениях, предоставляется возможность поработать с линиями или присутствующими столбцами.

Отдельный раздел называется «Параметры текста», где изменяется цвет надписей, общий стиль и другие опции. Посмотрите все настройки, которые здесь есть, чтобы подстроить внешнее отображение диаграмм под себя.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Увеличение/Уменьшение процентного соотношения

Когда число увеличивается относительно другого числа, то величина увеличения представляется как:

Увеличение = Новое число — Старое число

Однако, когда число уменьшается относительно другого числа, то эту величину можно представить как:

Уменьшение = Старое число — Новое число

Увеличение или уменьшение числа всегда выражается на основании старого числа.Поэтому:

%Увеличение = 100 ⋅ (Новое число — Старое число) ÷ Старое число

%Уменьшение = 100 ⋅ (Старое число — Новое число) ÷ Старое число

Например, у Вас было 80 почтовых марок и Вы начали в этом месяце собирать ещё пока общее количество почтовых марок достигло 120. Процентное увеличение числа марок, которые у Вас есть равно

$\frac{120 — 80}{80} \times 100 = 50\%$

Когда у Вас стало 120 марок, Вы и Ваш друг договорились обменять игру «Lego» на несколько из этих марок. Ваш друг взял несколько марок, которые ему понравились, и когда Вы подсчитали оставшиеся марки, то обнаружили, что у Вас осталось 100 марок. Процентное уменьшение числа марок может быть подсчитано как:

$\frac{120 — 100}{120} \times 100 = 16,67\%$