Сложные проценты в инвестировании: как с их помощью повысить доходность

Формула сложного процента

Формула сложного процента позволяет быстро и просто посчитать любую задачу на вклады. Выглядит эта формула так:

$S=X*(1+m)^{n}$, где

S – итоговая сумма вклада

Х – начальная сумма вклада

m-процент в виде десятичной дроби

n-количество периодов, за которые планируется получит прибыль.

Обратите внимание, что периоды могут быть месяцами, годами, неделями, кварталами и т.д. Это нужно учитывать при решении задач на сложный процент

Теперь подсчитаем, какую прибыль получит Петя за 10 лет.

X=10000

m=0,1

n=10

Подставим все в формулу:

$S=10000*{(1+0,1)^{10}}=25937 руб$ – результат округлен до целых чисел.

В процессе вычисления без калькулятора не обойтись, зато все расчеты производятся в два-три действия. Иногда по требованию учителя или составителя учебника, округление придется производить до сотых.

Что мы узнали?

Мы поговорили о том, что такое процент. Разобрались с определением сложного процента и привели формулу сложного процента. Привели небольшой пример сложного процента, результат которого нашли с помощью формулы.

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Расчет

Общая сумма, которую получит вкладчик, при расчёте по сложному проценту будет равна , где  — начальная сумма вложенных средств, — годовая процентная ставка,  — срок вклада в годах. При вкладе по ставке s% годовых, после первого года хранения капитал составил бы x плюс s% от неё, то есть возрос бы в раза. На второй год s% рассчитывались бы уже не от одной копейки, а от величины, большей её в (1 + s/100) раза. И, в свою очередь, данная величина увеличилась бы тоже за год в (1 + s/100) раза. Значит, по сравнению с первичной суммой вклад за два года возрос бы в раз. За три года — в раз.

К году N первичный вклад вырос бы до величины в раз больше первоначальной.

В применении к ежемесячной капитализации формула сложного процента имеет вид:

где x — начальная сумма вклада, s — годовая ставка в процентах, m — срок вклада в месяцах.

Это интересно: Формула расчета неустойки — рассмотрим развернуто

Использование офисных программ для работы со сложными процентами

Любой офисный пакет, а именно его табличный процессор, предоставляет множество функций для денежных расчетов: от самых простых и до самых сложных. Достаточно просто выбрать нужную (или несколько) для составления своих формул. Если использовать возможность программировать на VBA в Excel, то можно получать более быстрые результаты при расчетах. Когда рассчитывается сложная процентная ставка, формула может быть простейшей рекурсией без всяких степеней и логарифмов. Все сделает цикл с параметром в число периодов начисления. При необходимости можно легко добавить сумму периодического инвестирования, не ломая голову над выводом или поиском формул.

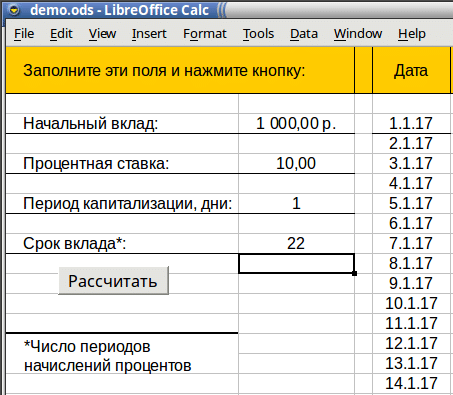
В примере, показанном ниже, используется, правда, не MS Excel, а LibreOffice Calc, – близнец Экселя для UNIX-подобных операционных систем. Но это, в принципе, ничего совершенно не меняет. Код макроса для OOBasic хоть и отличается от экселевского, но только в технических деталях.

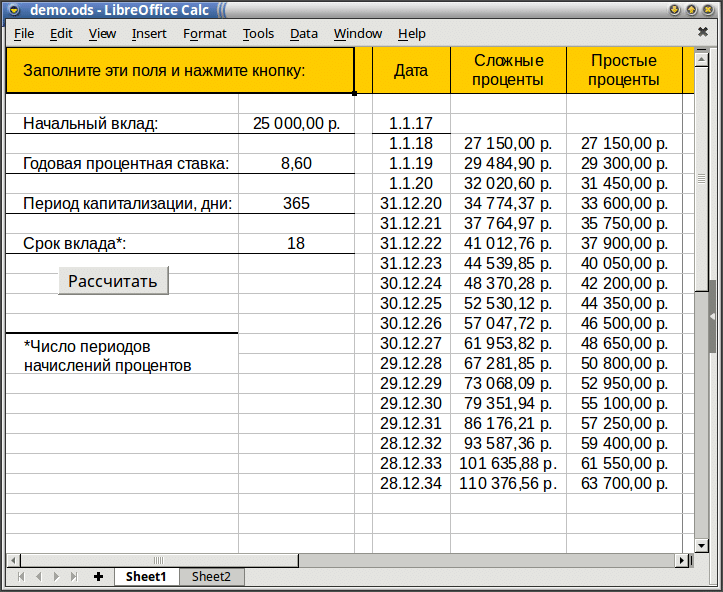
В примере на рисунке выше мы рассчитываем как сложные, так и простые проценты по вкладу 8,6% годовых. Проценты начисляются каждый год, а вклад рассчитан на 18 лет вперед. Начальный взнос 25 тыс. рублей мы (условно) делаем 1 января 2017 года. Если мы хотим сравнить графики для этих результатов, что, конечно, более наглядно, то добро пожаловать на следующий лист, в который этот самый график очень легко вставить.

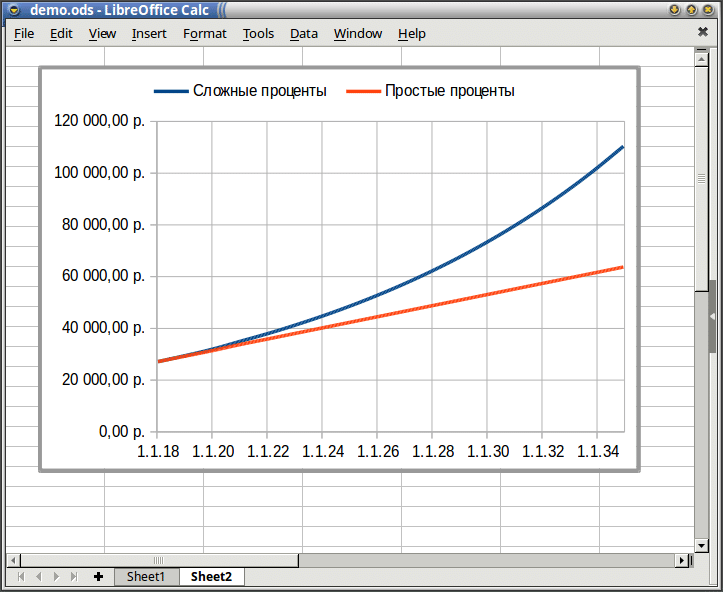
Пример показывает, что за прошедший срок составные проценты вдвое превышают простые.

Еще один пример. Можно легко переделать нашу модель и снять ограничение на ежегодную капитализацию. Тогда мы можем решить еще одну задачу. Предположим, что мы открыли центовый счет на бирже Forex и хотим поучаствовать в торговле валютами. Считая, что мы умеем, добросовестно работая с информацией, расти на 10% в день (что, может быть, слегка самонадеянно, но бог с ним), посмотрим, что получится из депозита в одну тысячу рублей, за месяц, т.е. 22 рабочих дня. Для этого чуть изменим формулу для нашего постоянного множителя:

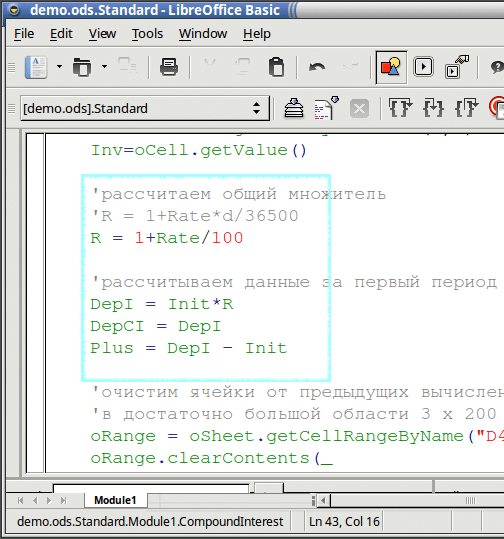
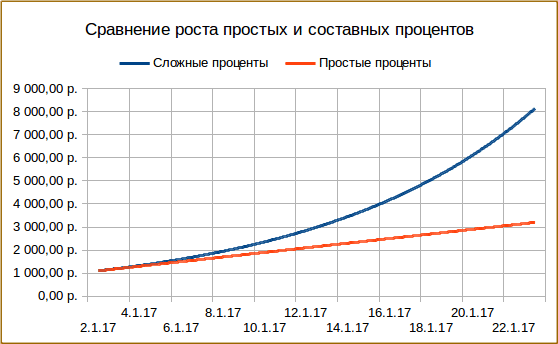
Теперь мы избавились от (довольно искусственного) ограничения на ежегодный пересчет процентов. И получаем такую картину:

А на графике можем видеть рост и разницу между составными и обычными процентами:

И здесь видна разница между простыми и составными процентами.

Как воспользоваться сложным процентом?

Стоит сразу поставить точки над i и уточнить, что принцип сложного процента касается не только инвестиций. Это общая формула, которую можно применить к работе, учебе, личным отношениям, да чему угодно. Подумайте сами, когда человек годами занимается определенным делом, отдаваясь ему на все сто – он планомерно и стабильно увеличивает свой опыт. Конечно, и возрастные изменения дадут о себе знать. Но, скажем так, с тренировками и упорным трудом, каждый может добиться значимого результата.

Личное развитие

Касательно языков. Учите по три слова в день, и через год Ваш словарный запас перевалит за 1000 слов. Особо актуально в канун Нового Года. Более того, регулярная практика вынудит Вас познавать и азы грамматики, строения лексики, функционированию языка и так далее. Иными словами, узкий аспект широкого поля действия не только позволит совершенствоваться исключительно в этой парадигме, но и расширять и углублять свои познания как личности.

Другой пример – регулярные физические тренировки. Нет разницы: силовые, кардио, кроссфит. По мере развития Ваших физических навыков, будут расти и когнитивные возможности. Мозг будет чаще омываться кровью, богатой кислородом, и лучше работать. Кстати, именно это и послужило развенчанию мифа про «тупых спортсменов».

И наоборот. Все гении, которые выходили на Нобелевские премии, признавали необходимость физических нагрузок. Все потому, что и научный труд, и физический, и стремление приумножить капитал в инвестировании стоят на системном принципе.

Инвестирование и сложный процент

Здесь речь идет о заработке и деньги – это основной механизм, в котором Вы можете протестировать теорию сложного процента. Всё, что Вам понадобится, это:

• Выбрать интересный для Вас тариф. Помните, чем выше будет сумма инвестиции – тем быстрее вы сможете выйти на полноценный пассивный доход;
• Приобрести его, и воспользоваться сопутствующими гарантиями для сохранности права на прибыль и защиты Вашего актива;
• Сохранять процентные выплаты.

На счет последнего пункта. Стратегия инвестирования позволяет как держать крупную сумму в постоянном обороте, так и снимать некий процент, тем самым поощряя себя, но и увеличивая грядущую прибыль. Подумайте сами, что более приоритетно для Вас сейчас? Получить немного денег, или стать полностью финансово независимым через год-два-три?

Если Вы достаточно независимы, воспользуйтесь этим инвестиционным механизмом.

Еще больше примеров

Выглядит это так: конечная сумма равна начальной, умноженной на сумму единицы и числа равного процентной ставке деленной на 100, в степени равной периоду на который осуществляется вложение (конечная сумма = начальная сумма * (1 + %)n).

В качестве примера не найти ничего лучшего, чем вклад денег на срочный депозит. В реальности для расчета сложных процентов по вкладам банкиры, применяют совершенную формулу имеющую вид: конечная сумма равна, начальной умноженной на единицу плюс процентная ставка деленая на 100, умножить на количество дней, деленное на количество дней в году, все в степени равной периоду вклада (конечная сумма = начальная сумма * (1 + p*d/y)n.

Другими словами, если вы вложили 1000 рублей под 12% годовых, то через год вы получите 1120 рублей. Если на второй год вы продлите вклад не с 1000 рублей а с 1120, то вместо 120 рублей вы уже получите 134,4 р. Кажется не большая разница, но вот что будет за 50 лет:

• Через З года — 1400
• Через 4 года — 1570
• Через 10 лет — 3100
• Через 20 лет — 9640
• Через З0 лет — 29 960
• Через 40 лет — 93 050
• Через 49 лет — 258 040
• Через 50 лет — 289 000

Однако все познается в сравнении и чтобы в полной мере оценить могучий потенциал того, что называется реинвестированием, необходимо сравнить, какие же результаты дают простые и сложные проценты. Если простые проценты дают линейный прирост прибыли, то реинвестиции – это экспоненциальное увеличение капитала, которое тем сильнее, чем большая сумма под больший процент и на дольший срок была вложена.

При необходимости из указанной выше формулы по расчету сложных процентов по банковским вкладам легко выводятся и формулы для определения других необходимых величин: действующей процентной ставки ((конечная сумма/ начальную сумму)1/n – 1); периода, за который из имеющейся суммы потребуется получить искомую (n = log(1+процентная ставка) (конечная сумма / начальную сумму)).

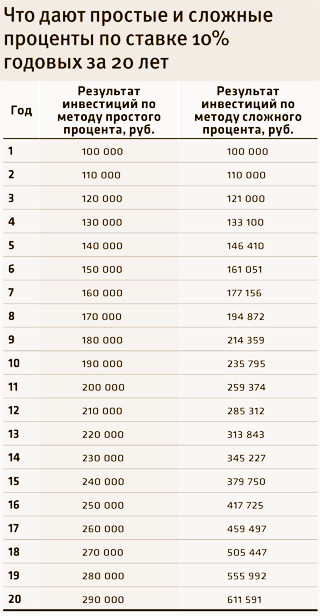
Все бы было здесь прекрасно, если бы не одно «но» – для того, чтобы сложные проценты действительно раскрыли свой полный потенциал и начали наращивать хорошую прибыль, требуется довольно продолжительный срок либо очень высокая процентная ставка, что в честных проектах встречается крайне редко.

А вот пример того, как можно заработать 1 миллион долларов за 11 лет, при условии первоначального вклада три тыс. долларов по 50% годовых, и ежемесячно нужно докладывать по 300 долларов (3600 в год):

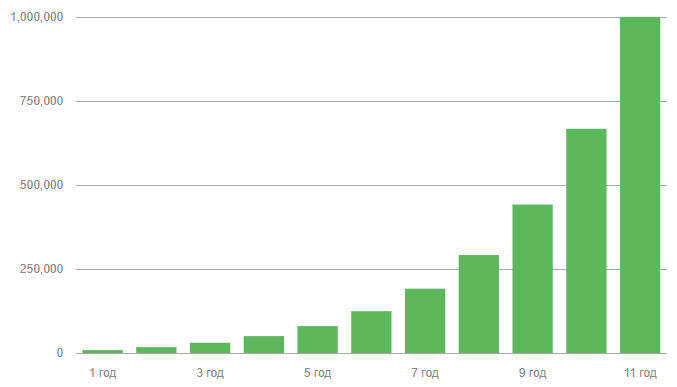
1 год $8 5652 год $17 3623 год $30 5584 год $50 3515 год $80 0426 год $124 5777 год $191 3818 год $291 5869 год $441 89310 год $667 35511 год $1 001 032

Простые проценты

Чтобы понять суть явления, разберёмся с его определением, рассмотрим пример и ознакомимся с формулой, по которой простые проценты высчитываются. Об этом ниже.

Общая суть

Если говорить простыми словами, ПП – зачисление платежа в награду за хранение вклада на счёте в банке за весь период действия реквизита.

Важно! ПП можно получить только после завершения действия депозитного соглашения. Они определяются годовой ставкой по процентам

Примечание 1. Когда договор в автоматическом режиме пролонгируется на очередной период, вознаграждение за предыдущий не прибавляется к телу депозита.

Пример 1. Клиент положил на счёт в кредитно-финансовой организации сумму в 50 000 российских рублей под 7% годовых. Срок – один год. Когда действие договора подошло к концу, прибыль составила: 50 000 * 0,07 = 3 500 руб. Если соглашение автоматически продлено, для следующего периода прибыль снова будет равна 3 500. Итого через два года в банке получится забрать 50 000 + 3 500 * 2 = 57 000.

Формула

Для понимания данной схемы начисления прибыли в целом нужно запомнить формулу. Для простых процентов она такая: K = D * p.

Что означают элементы:

• K – это суммарный итог по прибыли;
• D – депозитное тело;
• p – ставка по процентам за год.

Примечание 2. Учитывайте, что для расчётов нужно годовой процент делить на 100. Т.е. 7% = 0,07.

Если речь идёт о вкладе, который создан на срок менее года, p следует делить на количество месяцев в году (12) и умножать потом на количество месяцев, на протяжении которых деньги хранились на счёте в банке.

Пример 2. Период действия депозита – 3 месяца, ставка по процентам – 10%, сумма – 50 000 руб. Тогда: 50 000 * (0,1 / 12 * 3) = 1 250 руб. Такую сумму Вы получите в качестве прибыли за время активности договора.

0,1 – это 10% ставки, 3 – срок соглашения (количество месяцев).

Несмотря на все эти цифры и буквы, процедура расчётов совсем несложная. Главное – быть внимательными и подставлять нужные значения, а также корректно производить все вычисления.

Всё сказанное говорит о том, что простая схема в теории – для тех пользователей банковского сервиса, кто имеет необходимость в относительно краткосрочных вкладах. Продолжительное содержание депозита с простым начислением процентов не слишком выгодно. Хотя, как обычно, всегда есть свои весомые нюансы для каждого отдельного случая.

Сравнительная таблица

Основа для сравнения	Простой интерес	Сложный процент
Имея в виду	Простые проценты относятся к процентам, которые рассчитываются как процент от основной суммы.	Сложный процент относится к проценту, который рассчитывается как процент от основной суммы и начисленных процентов.
Вернуть	Меньше	Сравнительно высокий
принципал	постоянная	Продолжает меняться в течение всего периода заимствования.
рост	Остается однородным	Быстро увеличивается
Проценты начисляются на	принципал	Основной + накопленный интерес
формула	Простой интерес = P * r * n	Сложный процент = P * (1 + r) ^ nk

Дисконтирование

Дисконтирование – это процесс определения текущей стоимости денег, когда известна их будущая стоимость. Дисконтирование дохода применяется для оценки будущих денежных поступлений (прибыль, проценты, дивиденды) с позиции текущего момента.

Дисконтирование выполняется путём умножения будущих денежных потоков (потоков платежей) на коэффициент дисконтирования:

Экономический смысл дисконтирования (на примере)

Через 2 года Вам нужно будет 1 000 000 рублей, чтобы купить автомобиль. У Вас есть возможность положить деньги в банк под ставку 10%. Какой суммой денег нужно обладать сейчас, чтобы в будущем купить автомобиль?

Нам нужно будет 826 446,29 рублей, чтобы сейчас их инвестировать с доходность в 10% ежегодно  и через 2 года снять 1 000 000 рублей.

Проверим это:

826 446.29 * 1.1*1.1 = 1 000 000 рублей.

Простые проценты

На практике применяются

три варианта расчета

простых процентов:

• точные проценты с точным числом дней ссуды (английская практика). Обозначается как 365/365 или АТС/АТС.
• обыкновенные (коммерческие) проценты с точным числом дней ссуды (французская практика). Обозначается как 365/360 или АТС/360.
• обыкновенные проценты с приближенным числом дней ссуды (германская практика). Обозначается как 360/360. По схеме 360 количество дней к году принимается равным 360 (в каждом месяце по 30 дней).Пример. Определить приближённое число дней между 12.02.2019 и 27.08.2020.Если год рассматривается как промежуток, содержащий 12 месяцев продолжительностью 30 дней (дивизор равен 360 дней), то приближённое число дней рассчитывается следующим образом:n = 360*(y2-y1)+30*(m2-m1)+(d2-d1)где y – номер года, m – номер месяца в году, d – номер дня в месяце.n = 360*(2020-2019)+30*(8-2)+(27-12) = 555 дней

Наращение основной суммы: S = P(1+i*n)где P – исходная сумма, i – проценты, n – количество лет.

Когда срок финансовой сделки не равен целому числу лет:S=P·(1+tT​·i)где t – срок в днях, T – временная база (365 или 360)

Примеры задач на простые проценты

Выберите необходимый вид задачи (кнопка Решить) и заполните требуемые поля.

1. Ссуда в размере P = 1 млн.руб. выдана d1 = 20.01 до d2 = 05.10 включительно под i = 18% годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? При решении применить три метода расчёта срока ссуды.Решить аналогичнуюНачальная дата: 20.01, конечная дата: 05.10, количество дней между датами: 258Январь, 11 дней: с 21.01 по 31.01Февраль, 28 дней: с 01.02 по 28.02Март, 31 день: с 01.03 по 31.03Апрель, 30 дней: с 01.04 по 30.04Май, 31 день: с 01.05 по 31.05Июнь, 30 дней: с 01.06 по 30.06Июль, 31 день: с 01.07 по 31.07Август, 31 день: с 01.08 по 31.08Сентябрь, 30 дней: с 01.09 по 30.09Октябрь, 5 дней: с 01.10 по 05.10Итого: 11 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 5 = 258S=P·(1+tT​·i)1) Точные проценты с точным числом дней ссуды (365/365)S=1 000 000·(1+258365​·0.18)=1 127 232.88 руб.2) Обыкновенные проценты с точным числом дней (365/360)S=1 000 000·(1+258360​·0.18)=1 129 000 руб.3) Обыкновенные проценты с приближённым числом дней (360/360)Количество дней между датами: 255Январь, 10 дней: с 21.01 по 30.01Февраль, Март, Апрель, Май, Июнь, Июль, Август, Сентябрь по 30 днейОктябрь, 5 дней: с 01.10 по 05.10Итого: 10 + 30*8 + 5 = 255S=1 000 000·(1+255360​·0.18)=1 127 500 руб.
2. Через d = 180 дней после подписания договора должник уплатит S = 310 тыс.руб. Кредит выдан под i = 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?Решить аналогичнуюP=S(1+tT​·i)​Находим современную стоимость P=310 000(1+180365​·0.16)​ = 287 328.59 руб.

Расчет простых процентов

Простые проценты применяются в ссудозаемных финансовых операциях продолжительностью до одного года. При использовании этой схемы начисление процентов осуществляется однократно с учетом неизменной базы расчета. Для исчисления применяет следующая формула:

FV=CFo×(1+n×r) ,

где  FV –будущая стоимость денежных средств,

r – процентная ставка,

n – срок начисления.

В том случае, когда продолжительность ссудозаемной операции меньше календарного года, то для расчета используется следующая формула:

FV=CFo×(1+t/T×r),

где t – продолжительность операции в днях,

Т – общее количество дней в году

Сложный процент с ежемесячным пополнением вклада

Почему у клиентов банков часто возникают трудности со сложным банковским процентом? Чаще всего, потому, что они используют упрощенную формулу для расчета, и не учитывают разную ставку для каждого периода. Но тогда и общую формулу применять нельзя: ведь если в одном квартале у нас получится % = р * (90/365) = р * 0,2466, то уже во втором % = р * (91/365) = р * 0,2493.

Как посчитать сложный процент в таком случае? Вручную это делать долго и трудоемко, проще пользоваться программой Excel. Сначала рассмотрим другой вариант депозитного вклада – с ежемесячным пополнением.

Чем такой вклад отличается от стандартного депозита с капитализацией процентов? В данном случае по окончанию первого периода (месяца) к начальной сумме добавляются не проценты за этот период, а определенная фиксированная сумма. Для того чтобы посчитать сложный процент с ежемесячным пополнением, будем использовать другую формулу.

Для расчета сложного процента с пополнением формула выглядит так:

Сприбыль = Снач * (1 + %) w + (Сдоп* (1 +%) w+1 – Сдоп* (1 + %)) / % — Снач

Пример: вы положили на счет 100 000 рублей под 12% годовых, и каждый месяц добавляете к этому вкладу еще 5 000. При этом проценты мы не учитываем: считаем, что их вы получаете на отдельный счет и используете по-другому.

Вы получите: 100 000 * (1 +0,01) 12 – 100 000 + (5 000 * (1 + 0,01) 13 – 5 000 * 1,01) / 0,01 = 12 682 + 1904 = 14 586 рублей.

Чтобы посчитать сложный процент с капитализацией с точностью до дня, нужно рассчитывать каждый период отдельно, а затем суммировать их.

Формула для расчета по первому периоду: С1 = Снач * (1 + %). С1 – это не только проценты, но и плюс начальная сумма взноса. Расчет по второму периоду: С2 = С1 * (1 + %). Помните, что значение % в каждом случае будет разным.

Рассчитаем сложный банковский процент для вклада в 100 000 рублей под 12% годовых, с капитализацией каждый квартал. Днем, когда оформлен договор, будем считать 1 января.

С1 = Снач * (1 + %) = 100 000 * (1 + 0,12 * (30 + 28 + 31)/365) = 100 000 * (1 +0,12 * 0,2438356) = 100 000 * (1 + 0,0292603) = 102 926, 03 рублей;

С2 = 102 926,03 * (1 + 0,12 * (30 + 31 + 30)/365) = 102 926,03 * (1 + 0,0299178) = 106 005,35 рублей и т.д. Продолжая эти подсчеты, мы получим 112514,93 рублей. То есть, прибыль составит 12 514, 93 рублей (при подсчете по упрощенной формуле в итоге получалось 12 550 рублей).

Пользоваться такими сложными формулами не обязательно, разве что вы любите точные цифры и хотите проверить свой банк – правильно ли осуществляются начисления по вашим депозитам.

Расчет доли в процентах (удельного веса).

Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.

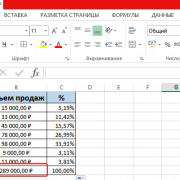
Пример 1. Сумма находится в конце таблицы в определенной ячейке.

Очень распространенный сценарий — это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.

Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы: 

=G2/$G$13

Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.

Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.

На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.

Пример 2. Часть итоговой суммы находится в нескольких строках.

В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.

В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:

Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:

Естественно, вы можете указать название товара прямо в формуле, например:

Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.

Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:

Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.

Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:

• Как использовать функцию СУММЕСЛИ в Excel
• СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями

Как сложный процент работает в инвестициях

Весьма доходные сложные проценты в инвестировании, например, в сегменте, онлайн, встречаются и не так редко, как это было 4, а то и 5 лет назад. Сложный процент максимально выгодный на длинной дистанции: что касаемо банков, то для депозитов на 5-10 лет, для проектов со среднесуточным начислением от 3% и работой вклада на бессрочной основе. Если самостоятельно сложно считать, то в сети множество калькуляторов, за пару секунд рассчитывающие размер сложных процентов и то, что получите на руки по истечению срока. Среди остальных инвестиций, где используется эта математическая формула начисления, можно выделить такие:

• облигации и вложение купонного дохода на очередной срок после даты N для выплат прибыли;
• дивидендные акции, приобрести которые можно через брокера, что является членом НАУФОР и выходит на разные биржи.

Правило простое: например, у вас есть пакет акций на 10 тыс. рублей и в год вы получаете 10%. За 10 лет вклад «окупится», если будете забирать прибыль, но, если примите решение аккумулировать ее, средняя окупаемость сократится до 7 лет.

Как работает сложный процент?

Сложный процент подразумевает использование начальной суммы и дохода, полученного во время предыдущих периодов. Таким примером может являться вклад в банке, в условиях которого указана капитализация полученной прибыли. Сумма процентов по вкладу, начисленная за первый месяц, добавляется к основному счёту, и во второй год процентная ставка применяется уже к увеличенной сумме, что обеспечивает рост итоговой прибыли.

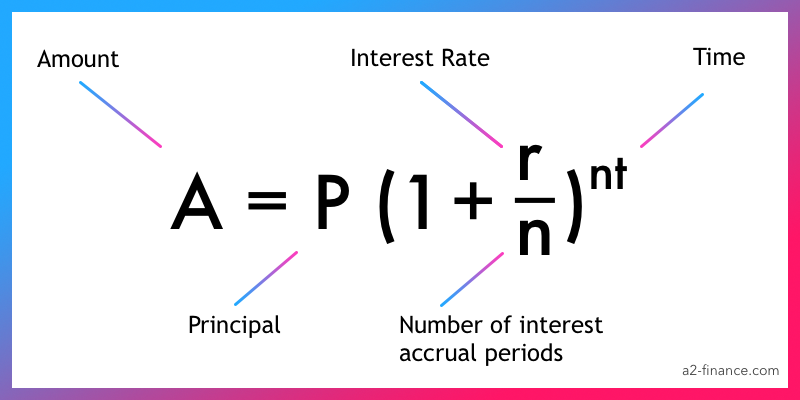
Формула сложного процента

Расчёт будущей прибыли при использовании сложного процента производится по формуле:

, где:

– сумма, которую вы получите в конце периода;

– сумма первоначальных инвестиций, т.е. то, что вы вкладываете;

– годовая ставка;

– количество периодов начисления ставки (ежемесячно, ежеквартально, ежегодно и т.д.);

– общий срок вклада в годах.

Пример сложных процентов

Как мы выяснили выше, при использовании сложных процентов, прибыль по вкладу постоянно увеличивается. Сейчас посмотрим на примере, как это происходит.

Предположим, что у нас открыт вклад на сумму в 1000$ на 1 год со ставкой 5%. В этом случае, доход в конце года будет: 1000$ + 1000$ * (5 / 100) = 1050$. То есть мы просто посчитали простой процент для вклада на один год. Затем мы решили, что хотим снова открыть вклад ещё на 1 год. Тогда мы возьмём полученные ранее 1050$ и снова добавим их на вклад под 5% годовых. Тогда получится: 1050$ + 1050$ * (5 / 100) = 1102.5$.

Как видите, в первый год мы получили 1050$, а на второй год 1102$. Это и есть пример работы сложного процента, т.е. когда результат первого года (те самые 1050$), мы использовали для процента второго года и тем самым получили 1102$.

Если бы во второй год мы использовали простой процент, то мы брали не результат прошлого года (1050$), а взяли снова 1000$. И получилось бы:

• 1 год: 1050$
• 2 год: 1050$
• 3 год: 1050$
• 4 год: 1050$
• 5 год: 1050$

Спустя 5 лет, на вашем депозите будет 5250$. А вот как меняется ваш депозит, если используется сложный процент:

• 1 год: 1050$
• 2 год: 1102$
• 3 год: 1157$
• 4 год: 1215$
• 5 год: 1276$

То есть, спустя 5 лет, на вашем депозите будет 5800$. Как вы видите, разница существенна и именно в этом магия сложного процента. Чем дольше вы вкладываете деньги, используя прибыль, накопленную за предыдущие года – тем выше будет доход в конце.

Разница между простым и сложным процентами

Основная разница между двумя типами процента в том, на что именно начисляется процент. Когда используется простой, то за основу вычислений всегда берётся первоначальная сумма

Неважно, делаете вы расчёт для первого года или третьего – сумма всегда одна. Для сложного же процента – основа вычислений, это результат предыдущих вычислений

То есть то, что вы рассчитывали для прошлого года, берётся за основу расчётов для текущего года. Кратко: простой процент – основа всегда одинакова, сложный процент – основа всегда разная.

Отличия между сложными и простыми процентами

Простой процент	Сложный процент
Доход начисляется один раз – в конце срока	Доход начисляется каждый год
При расчёте учитывается только начальная сумма	При расчёте учитывается начальная сумма плюс доход каждого года
Прибыль каждый год будет одинаковая.	Прибыль каждый год будет увеличиваться, то есть она всегда разная.