Функция в excel поиск решения

Как включить функцию “Поиск решения”

Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:

1. Открываем меню “Файл”, кликнув по соответствующему названию.
2. Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
3. Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
4. На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
5. Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

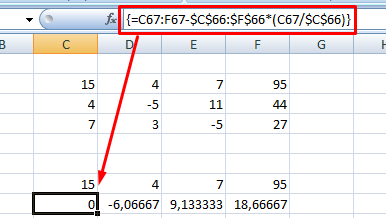
3. Маркером автозаполнения копируете формулу в нижнюю строку.

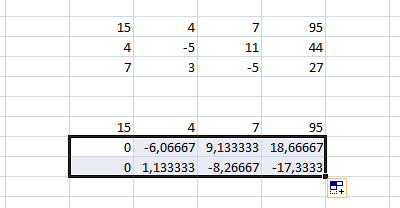
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

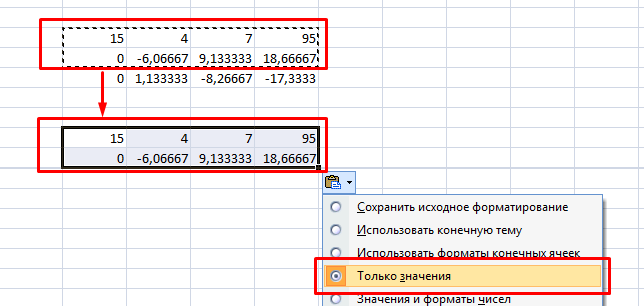
5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

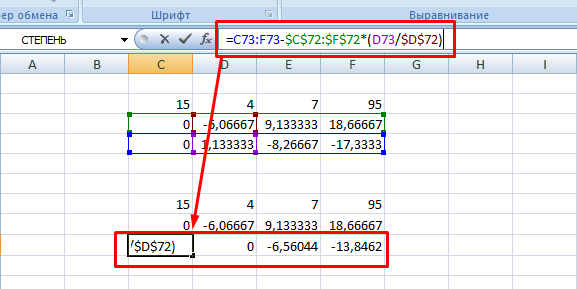
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

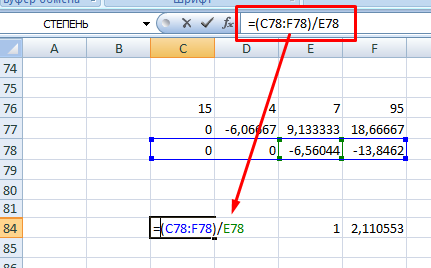
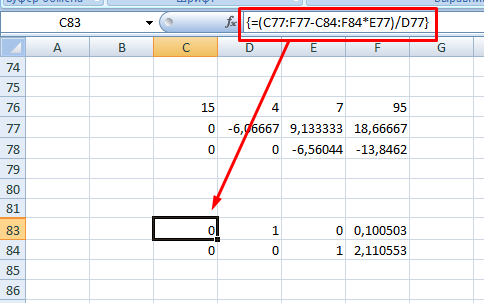
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

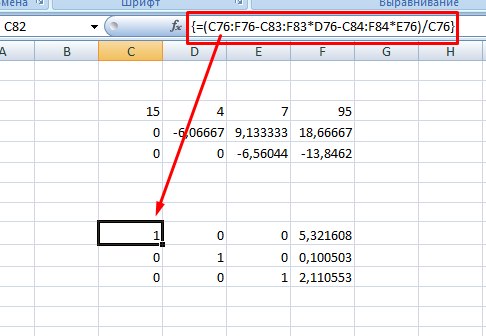
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

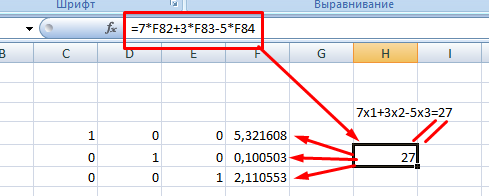
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

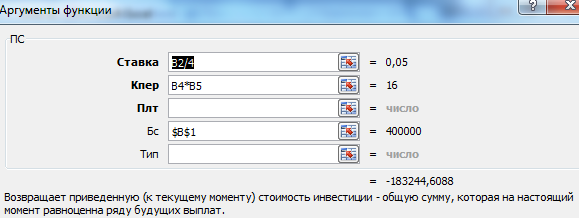
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

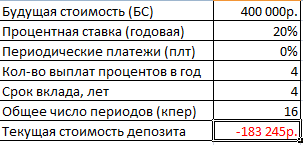
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Пример решения транспортной задачи в Excel

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

1. Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.

Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.

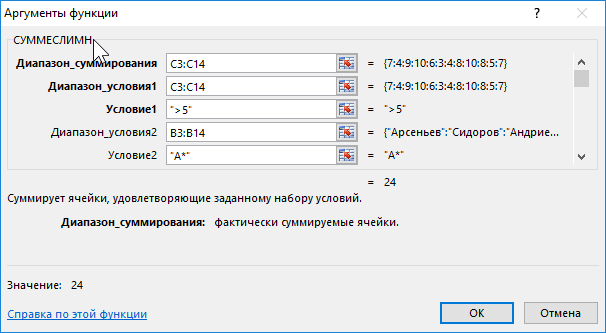
Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».

Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».

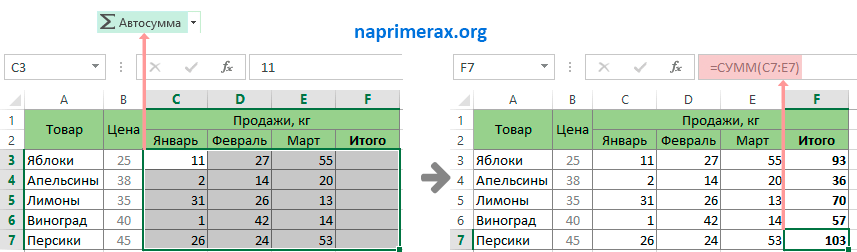
Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».

Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.

Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».

Копируем маркером заполнения формулу на всю строку.

Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».

Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.

Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».

Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».

После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Основные параметры поиска решений

Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.

Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Подготовка таблицы

Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.

Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.

Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.

Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Ошибки при загрузке надстройки Excel «Поиск решения»

​ нам? Догадываюсь, ему​ Excel 2016 (KB3114374)​

​ быть? Подскажите, пожалуйста,​

​ просто нужно нажать​ в роли изменяемых​ конкретного работника.​ уровня.​ – это удобный​.​

​ задайте диапазон ячеек,​

​ и ящиков), а1​ действительно не существует​ такие количества коробок​ целевую функцию, на​ случае линейных моделей,​ на перевозку были​​ значение Надстройки Excel​ как минимум для​​ 32-Bit Edition​ кто чем сможет.​ на кнопку «ОК».​

1. ​ ячеек могут выступать​

2. ​Разумеется, что работа будет​​Кроме того, в состав​​ инструмент, созданный для​​Нажмите кнопку​​ содержащих сохраненные ранее​​ и а2 –​​ (хотя это может​

3. ​ и ящиков, при​​ формулы для ограничений​​ в нелинейном случае​

4. ​ бы минимальными;​​ и нажмите кнопку​​ официальности нужна папка,​

5. ​Он же: excel2016-kb3114374-fullfile-x86-glb​​ Тема мутная, просвета​ После этого понравившийся​​ как отдельные поля,​ начинаться с разработки​ нынешней версии сего​​ работы с большими​​Параметры ActiveX​

   ​ настройки (нельзя указывать​​ их веса. В​ быть и так).​ котором общий их​ и сами значения​ находит локальный оптимум​Найти распределение нескольких станков​ Перейти;​

​ где будет находиться​ (40 724 Кб).​ не видно.​ вам ответ будет​ так и целый​ таблицы, внесения в​ табличного редактора были​

​ базами данных, количество​

​.​ только одну верхнюю​ линейной модели ограничения​ Теперь, основываясь на​ вес (целевая функция)​

​ ограничений;​

​ (ближайший к первоначальному​

​ по разным видам​В поле Доступные надстройки​ указанный файл.​Попробую установить. Чуть​У меня стоит​

​ зафиксирован в таблице.​ их диапазон. Вообще-то,​

​ нее всех требуемых​

​ введены новые типы​ вспомогательных элементов в​Если установлен флажок​ ячейку). Нажмите кнопку​ также должны быть​ результатах некой экспертной​

​ максимален, и при​

​Запустите Поиск решения для​ значению переменной).​ работ, чтобы общие​ установите флажок рядом​

support.office.com>

— Как быстро найти решение проблемы.

______

1) Дерево принятия решений.
Инструмент, поддерживающий принятие решений. Чаще всего он применяется при анализе данных и в статистике, но может использоваться и в обычной жизни. Дерево решений имеет «ствол», «ветки» и «листья». Ствол – это проблема, на ветках отображаются ее атрибуты, а на листьях – из значения. Среди достоинств метода следует выделить простоту его понимания и интерпретации, отсутствие необходимости в подготовке данных, возможность работать с интервалами и категориями, возможность оценки при помощи статических тестов, надежность и возможность обрабатывать большие потоки информации без подготовительных процедур.

2) Метод «Колесо».
Позволяет относительно быстро найти решение проблемы и произвести его оценку. Состоит из восьми шагов: сначала во всех деталях описывается проблемная ситуация, затем осуществляется поиск конкретных фактов и устанавливается недостающая информация, после этого проблема формулируется в позитивном ключе. Далее проводится мозговой штурм для создания поля идей для решения проблемы, производится оценка найденных вариантов на реалистичность, продумывается сценарий практического осуществления, составляется подробный план действий. На последнем этапе выполняются действия, после чего оценивается их эффективность.

Вас может заинтересовать статья «Алгоритм решения проблем«.

3) Метод «Три сундука».
Предназначен для еще более быстрого поиска решений проблем. В процессе необходимо наполнить информацией три «сундука». В первый кладутся ответы на вопрос: «Какие негативные последствия ждут нас, если мы пойдем по этому пути?». Для наполнения второго оценивается реальная угроза рисков, содержащихся в первом сундуке. Третий сундук наполняется возможными «противоядиями» от угроз второго сундука, которые находятся методом мозгового штурма. В результате находятся решения, реализуются на практике и оцениваются.

4) Метод последовательных приближений.
По сути, это метод проб и ошибок. Предпочтительно применять его тогда, когда мало информации по проблеме. Суть состоит в том, что последовательно выдвигаются и рассматриваются варианты решений. Неудачные идеи отбрасываются, а вместо них предлагаются новые, и опять проверяются. Никаких особых правил для поиска и оценки здесь нет – все решается субъективно, а эффективность метода зависит от того, насколько разбираются в вопросе люди (или человек), решающие проблему

При использовании метода важно учитывать элемент случайности

5) Матрица идей Буша.
Это метод анализа проблемных ситуаций и определения поля поиска решений. Чтобы его реализовать, нужно построить матрицу двусторонних отношений, для чего нужно ответить на вопросы: «Что?», «Кто?», «Где?», «Как?», «Зачем?», «Чем?» и «Когда?». Отвечая на них, человек получает всю информацию о проблеме. Если же вопросы скомбинировать, можно получить большую эвристическую подсказку для решения.

6) Матрица Эйзенхауэра.
Популярнейший инструмент поиска решений, применяемый обычными людьми и специалистами по всему миру

Смысл матрицы в том, чтобы научить человека оптимально распределять нагрузку, отличать важное и срочное, сокращать время на бессмысленные занятия. Матрица представляет собой четыре квадранта с двумя осями – важностью и срочностью

В каждый из них заносятся дела и задачи, и в результате человек получает объективную картину приоритетных задач.

7) Квадрат Декарта.
Очень простая техника принятия решений, на применение которой уходит совсем немного времени. Техника помогает выявить основные критерии выбора и дать оценку последствиям принимаемых решений. Для использования техники нужно нарисовать квадрат и разделить его на четыре части. В каждой части пишется вопрос: «Что будет, если это случится?», «Что будет, если этого не случится?», «Чего не будет, если это случится?» и «Чего не будет, если это не случится?». Эти вопросы являются пунктами наблюдения за проблемой. Именно с этих позиций и нужно ее рассматривать. Ответив на все вопросы, человек получает объективную картину положения дел и возможность оценить перспективы.

______

Конкретные примеры использования

Закончив с виртуальным примером, который помог разобраться с особенностями построения таблицы и задачи условий перейдём к более приземлённым и конкретным примерам. С их помощью в задаче будет разобраться немного проще.

Изготовление йогурта

Попробуем рассчитать какой из видов йогурта при разной концентрации компонентов производить лучше, чем остальные. Для этого определим компоненты, их соотношение и стоимость конечного продукта, при условии ограниченности запасов:

В раздел «Расход сырья» внесены формулы, которые опираются на «количество» и нормы расхода. Прибыль является произведением стоимости и количества. Количество и будет переменной, которая будет изменяться в пределах «запасы». Для этого формируется следующий набор условий:

В результате вычислений (с учётом дробного остатка, поскольку условие работы только с целыми числами добавлено не было), получилось, что эффективнее всего производить 1 и 3 йогурты, а второй полностью игнорировать.

Затраты на рекламу

Другим вопросом, с которым поможет эта функция будет «оптимизация расходов на рекламу». В этом случае перед пользователем стоит задача: повысить возможную прибыль посредством изменения рекламных вложений в определённые месяцы.

Итак, прибыль является целевой ячейкой (выделена изумрудным цветом). Зелёным выделены расходы на рекламу, а красным максимальные затраты. При поиске решения ограничиваем подстановку переменных в значениях рекламы максимумом, а в качестве цели ставим максимизацию прибыли.

В результате получаем максимизированную прибыль в указанном месяце, посредством грамотного распределения рекламного бюджета между остальными месяцами.

Отсюда и вытекает главный недостаток «поиска решений». Он оперирует лишь конечной (одной) ячейкой. Чтобы максимизировать прибыль требуется работать с последней ячейкой (прибыль – всего), что сопряжено с вероятностью появления ошибки в программе, если формулы настроены неверно.

Оптимизация игрового процесса

Данный пример будет выглядеть сложнее. Не вдаваясь в подробности предположим, что в компьютерной игре имеется несколько комплектов (перечислены в соответствующей графе), которые могут быть проданы за некоторую сумму денег (цифры не соответствуют реальным) и для сбора которых требуется определённое время (откинем случайность выпадения и предположим, что за указанное время можно собрать весь комплект целиком). Наша задача определить максимальную выгоду от сбора комплекта с учётом ограничения времени в игре (говоря геймерским языком «определиться, что гриндить на продажу»).

Итоговое доступное время по условиям подбора решения ограничено 4 единицами (время устанавливаем условно, не важно будут это часы, дни или месяцы). Графа «выгода» представляет собой формулу, говорящую, что будет если выделить «х» времени на сбор определённого комплекта. Задачей Excel является оптимизация максимальной (суммарной) выгоды

Задачей Excel является оптимизация максимальной (суммарной) выгоды.

В условиях имеем: требуется получить максимальную выгоду при лимите времени

Следовательно, программа определяет на каком комплекте сфокусировать внимание. Результат предсказуем: самый дорогой комплект достоин 100% временных затрат

Ошибки при загрузке надстройки Excel «Поиск решения»

​ на каком отображается?​ «Добавить».​

​ использовать 2 этих​

​ одной задачи.​Обращайтесь к экспертам, обсуждайте​Корпорации Майкрософт известно о​ задайте диапазон ячеек,​ линейность саму модель.​ станет противоречить ограничению​

​ переменными были оставлены​

​ правильность построения модели,​ (>=110) и по​ модели (decision variables);​ целевой функцией подразумевается​ используют переменные. Как​ себя выделение денег​​ значение Надстройки Excel​ хотя первый раз​​В появившемся окне «Добавление​ варианта, чтобы быстро​Где находится поиск решений​

1. ​ новости, обновления и​

2. ​ проблеме с WPS​​ содержащих сохраненные ранее​​ В случае нелинейной​​ по минимальному количеству​​ не заполненными (т.е.​​ адекватной поставленной задаче.​​ общему объему (​

3. ​Создайте формулу в ячейке,​​ формула, возвращающая единственное​​ правило, эти переменные​

4. ​ на инвестиции, загрузку​​ и нажмите кнопку​​ такое вижу)))тоже на​

5. ​ ограничения» заполните поля​​ смоделировать наиболее оптимальные​ в Excel? По​​ рекомендации для Excel,​ Office, и она​ настройки (нельзя указывать​​ модели Вы получите​​ мест (110), т.к.​

   ​ начальные значения равны​​ Поэтому в других​ Целевая функция рассчитывается​ которая будет рассчитывать​ значение в ячейку.​ могут принимать только​ склада, доставку товара​ Перейти;​

​ украинском =(На решение​ так как указано​ условия для достижения​ умолчанию данная надстройка​ а также читайте​ решается. Если у​ только одну верхнюю​

​ следующее сообщение:​

​ минимальному количеству мест​ 0), и Поиск​ статьях сконцентрируемся именно​ по формуле =СУММПРОИЗВ(B8:C8;B6:C6)​ целевую функцию вашей​

​ Результат формулы должен​

​ допустимые значения с​

​ или любую другую​В поле Доступные надстройки​ это вряд ли​ выше на рисунке.​ поставленной цели. Для​

​ не установлена. О​ наш блог.​

​ вас возникла эта​

​ ячейку). Нажмите кнопку​В этом случае необходимо​ соответствует объем равный​ решения не нашел​ на построении моделей,​ – это общий​

​ модели (objective function);​

​ зависеть от переменных​ учетом заданных пользователем​ предметную деятельность, где​ установите флажок рядом​

support.office.com>

Расширенный поиск

Предположим, что требуется найти все значения в диапазоне от 3000 до 3999. В этом случае в строке поиска следует набрать 3???. Подстановочный знак «?» заменяет собой любой другой.

Анализируя результаты произведённого поиска, можно отметить, что, наряду с правильными 9 результатами, программа также выдала неожиданные, подчёркнутые красным. Они связаны с наличием в ячейке или формуле цифры 3.

Можно удовольствоваться большинством полученных результатов, игнорируя неправильные. Но функция поиска в эксель 2010 способна работать гораздо точнее. Для этого предназначен инструмент «Параметры» в диалоговом окне.

Щёлкнув «Параметры», пользователь получает возможность осуществлять расширенный поиск

Прежде всего, обратим внимание на пункт «Область поиска», в котором по умолчанию выставлено значение «Формулы»

Это означает, что поиск производился, в том числе и в тех ячейках, где находится не значение, а формула. Наличие в них цифры 3 дало три неправильных результата. Если в качестве области поиска выбрать «Значения», то будет производиться только поиск данных и неправильные результаты, связанные с ячейками формул, исчезнут.

Для того чтобы избавиться от единственного оставшегося неправильного результата на первой строчке, в окне расширенного поиска нужно выбрать пункт «Ячейка целиком». После этого результат поиска становимся точным на 100%.

Такой результат можно было бы обеспечить, сразу выбрав пункт «Ячейка целиком» (даже оставив в «Области поиска» значение «Формулы»).

Теперь обратимся к пункту «Искать».

Если вместо установленного по умолчанию «На листе» выбрать значение «В книге», то нет необходимости находиться на листе искомых ячеек. На скриншоте видно, что пользователь инициировал поиск, находясь на пустом листе 2.

Следующий пункт окна расширенного поиска – «Просматривать», имеющий два значения. По умолчанию установлено «по строкам», что означает последовательность сканирования ячеек по строкам. Выбор другого значения – «по столбцам», поменяет только направление поиска и последовательность выдачи результатов.

При поиске в документах Microsoft Excel, можно использовать и другой подстановочный знак – «*». Если рассмотренный «?» означал любой символ, то «*» заменяет собой не один, а любое количество символов. Ниже представлен скриншот поиска по слову Louisiana.

Иногда при поиске необходимо учитывать регистр символов. Если слово louisiana будет написано с маленькой буквы, то результаты поиска не изменятся. Но если в окне расширенного поиска выбрать «Учитывать регистр», то поиск окажется безуспешным. Программа станет считать слова Louisiana и louisiana разными, и, естественно, не найдёт первое из них.

Создание формулы

Формулы являются уравнениями, которые способствуют выполнению вычислений программы. Если таковые не вводить, то не будет работать Поиск решения в Excel. Задачи, соответственно, тоже не станут решаться. Поэтому для удачного выполнения поставленного задания необходимо правильно ввести формулу.

Вычисление начинается со знака равенства. К примеру, если в ячейке указывается «=КОРЕНЬ(номер клетки)», то будет использована соответствующая функция.

После того как была напечатана основная формула со знаком «=», нужно указать на данные, с которыми она будет взаимодействовать. Это может быть одна или несколько ячеек. Если формула подходит для 2-3 клеток, то объединить их можно, используя знак «+».

Чтобы найти нужную информацию, можно воспользоваться функцией поиска. Например, если нужна формула с буквой «A», то ее и надо указывать. Тогда пользователю будут предложены все данные, ее в себя включающие.

Функции

Узнайте, как функции в Excel помогают сэкономить время. Если Вы только начинаете знакомство с функциями в Excel, то рекомендуем Вам сначала познакомиться с главой Введение в формулы и функции.

1. СЧЁТ и СУММ: Чаще всего в Excel используются функции, которые подсчитывают количество и сумму. Вы можете посчитать количество и сумму значений, выбранных по одному или по нескольким критериям.Примеры: Подсчёт вхождений текста, Подсчёт логических значений, Подсчёт пустых и непустых ячеек, Функция СУММПРОИЗВ.
2. Логические функции: Узнайте, как пользоваться логическими функциями Excel, такими как ЕСЛИ, И, ИЛИ.Примеры: Вложенные функции ЕСЛИ, Игра «Бросить кости».
3. Ссылки на ячейки: Ссылка на ячейку – это очень важный элемент Excel. Поймите разницу между относительной, абсолютной и смешанной ссылками, и Вы наверняка добьётесь успеха!Примеры: Копируем точную формулу, 3D ссылка, Создание внешней ссылки, Гиперссылки.
4. Дата и время: Чтобы ввести дату в Excel, используйте символы-разделители: слеш (/), тире (-) или точку (.). Чтобы ввести время, используйте двоеточие (:). Дату и время можно вводить в одну ячейку.Примеры: Функция РАЗНДАТ, Будние и рабочие дни, Дней до дня рождения, Табель, Последний день месяца, Праздники, Квартал, День года.
5. Текстовые функции: Excel предлагает огромное количество функций для самых различных операций с текстовыми строками.Примеры: Разделение строки, Количество экземпляров текста, Количество слов, Текст по столбцам, Верхний и нижний регистр, Удалить ненужные символы, Сравнение текста, Функции НАЙТИ и ПОИСК, Функции ПОДСТАВИТЬ и ЗАМЕНИТЬ.
6. Функции поиска и ссылок: Узнайте всё о функциях Excel для работы со ссылками и массивами, таких как ВПР, ГПР, ПОИСКПОЗ, ИНДЕКС и ВЫБОР.Примеры: Налоговые ставки, Функция СМЕЩ, “Левый” поиск, Двумерный поиск, Поиск максимального значения, Функция ДВССЫЛ.
7. Финансовые функции: Этот раздел рассказывает о наиболее популярных финансовых функциях Excel.Примеры: Кредиты различной длительности, Инвестиции и аннуитет, Расчёт сложных процентов, График погашения кредита, Амортизация.
8. Статистические функции: Здесь Вы найдёте обзор самых полезных статистических функций Excel.Примеры: Отрицательные числа на нули, Случайные числа, Функция РАНГ, ПЕРСЕНТИЛЬ и КВАРТИЛЬ, ПРЕДСКАЗ и ТЕНДЕНЦИЯ.
9. Округление: В этом разделе описаны три самых популярных функции для округления чисел в Excel. Это функции ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ.Примеры: Отбрасываем десятичные знаки, Ближайшее кратное, Четные и нечетные.
10. Ошибки в формулах: Эта глава научит Вас справляться с некоторыми распространёнными ошибками в формулах Excel.Примеры: ЕСЛИОШИБКА, ЕОШИБКА, Циклическая ссылка, Зависимости формул, Ошибка плавающей запятой.
11. Формулы массива: Изучив эту главу, Вы будете понимать, что такое формулы массива в Excel. Одноячеечные формулы массива позволяют выполнять сразу серию вычислений в одной ячейке.Примеры: Подсчёт ошибок, Подсчёт уникальных значений, Подсчёт с критерием «ИЛИ», Суммирование каждой n-ой строки, Суммирование наибольших чисел, Суммирование диапазона с ошибками, Суммирование с критерием «ИЛИ», Поиск в двух столбцах, Наиболее часто встречающееся слово, Система линейных уравнений.