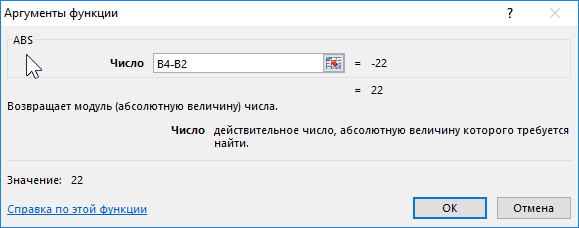
Псевдослучайные числа

Содержание:

Зачем нужны функции getstate() и setstate() ?
Выбор случайного элемента из списка choice() модуль random
Всё то же, только лучше: заголовок
Предыстория
Функция random() – «случайные» вещественные числа
Игра в кости с использованием модуля random в Python
QRandomGenerator
qrand
Функция srand().
Вопрос 3. Псевдослучайные числа
Random.hpp
Инициализация генератора и seed
Распределения
Функции для получения целых «случайных» чисел – randint() и randrange()
Случайности не случайны

Зачем нужны функции getstate() и setstate() ?

Если вы получили предыдущее состояние и восстановили его, тогда вы сможете оперировать одними и теми же случайными данными раз за разом. Помните, что использовать другую функцию random в данном случае нельзя. Также нельзя изменить значения заданных параметров. Сделав это, вы измените значение состояния .

Для закрепления понимания принципов работы и в генераторе случайных данных Python рассмотрим следующий пример:

Python

import random

number_list =

print(«Первая выборка «, random.sample(number_list,k=5))

# хранит текущее состояние в объекте state
state = random.getstate()

print(«Вторая выборка «, random.sample(number_list,k=5))

# Восстанавливает состояние state, используя setstate
random.setstate(state)

#Теперь будет выведен тот же список второй выборки
print(«Третья выборка «, random.sample(number_list,k=5))

# Восстанавливает текущее состояние state
random.setstate(state)

# Вновь будет выведен тот же список второй выборки
print(«Четвертая выборка «, random.sample(number_list,k=5))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

importrandom

number_list=3,6,9,12,15,18,21,24,27,30

print(«Первая выборка «,random.sample(number_list,k=5))

# хранит текущее состояние в объекте state

state=random.getstate()

print(«Вторая выборка «,random.sample(number_list,k=5))

# Восстанавливает состояние state, используя setstate

random.setstate(state)

#Теперь будет выведен тот же список второй выборки

print(«Третья выборка «,random.sample(number_list,k=5))

# Восстанавливает текущее состояние state

random.setstate(state)

# Вновь будет выведен тот же список второй выборки

print(«Четвертая выборка «,random.sample(number_list,k=5))

Вывод:

Shell

Первая выборка
Вторая выборка
Третья выборка
Четвертая выборка

1
2
3
4

Перваявыборка18,15,30,9,6

Втораявыборка27,15,12,9,6

Третьявыборка27,15,12,9,6

Четвертаявыборка27,15,12,9,6

Как можно заметить в результате вывода — мы получили одинаковые наборы данных. Это произошло из-за сброса генератора случайных данных.

Выбор случайного элемента из списка choice() модуль random

Числа. комплексные (мнимые) числа

Метод используется для выбора случайного элемента из списка. Набор может быть представлен в виде списка или python строки. Метод возвращает один случайный элемент последовательности.

Пример использования в Python:

Python

import random

list =
print(«random.choice используется для выбора случайного элемента из списка — «, random.choice(list))

1
2
3
4
5

importrandom

list=55,66,77,88,99

print(«random.choice используется для выбора случайного элемента из списка — «,random.choice(list))

Вывод:

Shell

random.choice используется для выбора случайного элемента из списка — 55

1	random.choiceиспользуетсядлявыбораслучайногоэлементаизсписка-55

Всё то же, только лучше: заголовок

Как округлять числа

Заголовок random разделяет генерацию псевдослучайных чисел на 3 части и предоставляет три инструмента:

класс std::random_device, который запрашивает у операционной системы почти случайное целое число; этот класс более удачные зёрна, чем если брать текущее время
класс std::mt19937 и другие классы псевдо-случайных генераторов, задача которых — размножить одно зерно в целую последовательность чисел
класс std::uniform_int_distribution и другие классы распределений

Класс mt19937 реализует алгоритм размножения псевдослучайных чисел, известный как Вихрь Мерсенна. Этот алгоритм работает быстро и даёт хорошие результаты — гораздо более “случайные”, чем наш самописный метод, показанный ранее.

О распределениях скажем подробнее:

линейное распределение вероятностей (uniform distribution) возникает, когда вероятность появления каждого из допустимых чисел одинакова, т.е. каждое число может появиться с равным шансом
в некоторых прикладных задачах нужны другие распределения, в которых одни числа появляются чаще других — например, часто используется нормальное распределение (normal distribution)

В большинстве случаев вам подойдёт линейное распределение. Изредка пригодится нормальное, в котором вероятность появления числе тем ниже, чем дальше оно от среднего значения:

Теперь мы можем переписать

Предыстория

Как округлять числа в excel

Все началось с того, что я заметил, как в игре, в которой уровни генерировались процедурно, противники начали вести себя одинаково каждый раз при восстановлении старого уровня (вышел из игры, при повторном заходе, тебе предложили продолжить). Когда уровень начинался заново у противников была одна и та же комбинация поведений: сначала налево, потом стреляют, потом от игрока и опять стреляют.

После долгого исследования плагина и кода поведения мобов я нашел проблемное место. Это была одна безобидная строчка в проекте с больше чем 100 сборками и больше чем 60000 строк кода.

Эта строка выглядела так:

По факту эта строка просто позволяла загрузить ранее сгенерированный уровень. Но неявно, так же, она проставляла один единственный seed для всего класса

Функция random() – «случайные» вещественные числа

Чтобы получить случайное вещественное число, или, как говорят, число с плавающей точкой, следует использовать функцию из одноименного модуля языка Python. Она не принимает никаких аргументов и возвращает число от 0 до 1, не включая 1:

>>> random.random()
0.17855729241927576
>>> random.random()
0.3310978930421846

или

>>> random()
0.025328854415995194

Результат содержит много знаков после запятой. Чтобы его округлить, можно воспользоваться встроенной в Python функцией :

>>> a = random.random()
>>> a
0.8366142721623201
>>> round(a, 2)
0.84
>>> round(random.random(), 3)
0.629

Чтобы получать случайные вещественные числа в иных пределах, отличных от [0; 1), прибегают к математическим приемам. Так если умножить полученное из число на любое целое, то получится вещественное в диапазоне от 0 до этого целого, не включая его:

>>> random.random() * 10
2.510618091637596
>>> random.random() * 10
6.977540211221759

Если нижняя граница должна быть отличной от нуля, то число из надо умножать на разницу между верхней и нижней границами, после чего прибавить нижнюю:

>>> random.random() * (10 - 4) + 4
9.517280589233597
>>> random.random() * (10 - 4) + 4
6.4429124181215975
>>> random.random() * (10 - 4) + 4
4.9231983600782385

В данном примере число умножается на 6. В результате получается число от 0 до 6. Прибавив 4, получаем число от 4 до 10.

Пример получения случайных чисел от -1 до 1:

>>> random.random() * (1 + 1) - 1
-0.673382618351051
>>> random.random() * (1 + 1) - 1
0.34121487148075924
>>> random.random() * (1 + 1) - 1
-0.988751324713907
>>> random.random() * (1 + 1) - 1
0.44137358363477674

Нижняя граница равна -1. При вычитании получается +. Когда добавляется нижняя граница, то плюс заменяется на минус ( +(-1) = — 1).

Для получения псевдослучайных чисел можно пользоваться исключительно функцией . Если требуется получить целое, то всегда можно округлить до него с помощью или отбросить дробную часть с помощью :

>>> int(random.random() * 100)
61
>>> round(random.random() * 100 - 50)
-33

Игра в кости с использованием модуля random в Python

Далее представлен код простой игры в кости, которая поможет понять принцип работы функций модуля random. В игре два участника и два кубика.

Участники по очереди бросают кубики, предварительно встряхнув их;
Алгоритм высчитывает сумму значений кубиков каждого участника и добавляет полученный результат на доску с результатами;
Участник, у которого в результате большее количество очков, выигрывает.

Код программы для игры в кости Python:

Python

import random

PlayerOne = «Анна»
PlayerTwo = «Алекс»

AnnaScore = 0
AlexScore = 0

# У каждого кубика шесть возможных значений
diceOne =
diceTwo =

def playDiceGame():
«»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»»

for i in range(5):
#оба кубика встряхиваются 5 раз
random.shuffle(diceOne)
random.shuffle(diceTwo)
firstNumber = random.choice(diceOne) # использование метода choice для выбора случайного значения
SecondNumber = random.choice(diceTwo)
return firstNumber + SecondNumber

print(«Игра в кости использует модуль random\n»)

#Давайте сыграем в кости три раза
for i in range(3):
# определим, кто будет бросать кости первым
AlexTossNumber = random.randint(1, 100) # генерация случайного числа от 1 до 100, включая 100
AnnaTossNumber = random.randrange(1, 101, 1) # генерация случайного числа от 1 до 100, не включая 101

if( AlexTossNumber > AnnaTossNumber):
print(«Алекс выиграл жеребьевку.»)
AlexScore = playDiceGame()
AnnaScore = playDiceGame()
else:
print(«Анна выиграла жеребьевку.»)
AnnaScore = playDiceGame()
AlexScore = playDiceGame()

if(AlexScore > AnnaScore):
print («Алекс выиграл игру в кости. Финальный счет Алекса:», AlexScore, «Финальный счет Анны:», AnnaScore, «\n»)
else:
print(«Анна выиграла игру в кости. Финальный счет Анны:», AnnaScore, «Финальный счет Алекса:», AlexScore, «\n»)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

importrandom

PlayerOne=»Анна»

PlayerTwo=»Алекс»

AnnaScore=

AlexScore=

# У каждого кубика шесть возможных значений

diceOne=1,2,3,4,5,6

diceTwo=1,2,3,4,5,6

defplayDiceGame()

«»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»»

foriinrange(5)

#оба кубика встряхиваются 5 раз

random.shuffle(diceOne)

random.shuffle(diceTwo)

firstNumber=random.choice(diceOne)# использование метода choice для выбора случайного значения

SecondNumber=random.choice(diceTwo)

returnfirstNumber+SecondNumber

print(«Игра в кости использует модуль random\n»)

#Давайте сыграем в кости три раза

foriinrange(3)

# определим, кто будет бросать кости первым

AlexTossNumber=random.randint(1,100)# генерация случайного числа от 1 до 100, включая 100

AnnaTossNumber=random.randrange(1,101,1)# генерация случайного числа от 1 до 100, не включая 101

if(AlexTossNumber>AnnaTossNumber)

print(«Алекс выиграл жеребьевку.»)

AlexScore=playDiceGame()

AnnaScore=playDiceGame()

else

print(«Анна выиграла жеребьевку.»)

AnnaScore=playDiceGame()

AlexScore=playDiceGame()

if(AlexScore>AnnaScore)

print(«Алекс выиграл игру в кости. Финальный счет Алекса:»,AlexScore,»Финальный счет Анны:»,AnnaScore,»\n»)

else

print(«Анна выиграла игру в кости. Финальный счет Анны:»,AnnaScore,»Финальный счет Алекса:»,AlexScore,»\n»)

Вывод:

Shell

Игра в кости использует модуль random

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 5 Финальный счет Алекса: 2

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 2

Алекс выиграл жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 8

1
2
3
4
5
6
7
8
9
10

Игравкостииспользуетмодульrandom

Аннавыигралажеребьевку.

Аннавыигралаигрувкости.ФинальныйсчетАнны5ФинальныйсчетАлекса2

Аннавыигралажеребьевку.

Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса2

Алексвыигралжеребьевку.

Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса8

Вот и все. Оставить комментарии можете в секции ниже.

QRandomGenerator

Применение QRandomGenerator будет следующим

#include <QCoreApplication>
#include <iostream>

#include <QRandomGenerator>

int main(int argc, char *argv[])
{
    QCoreApplication a(argc, argv);

    std::cout << "Random Qt 3 - ";
    QRandomGenerator generator;
    for (int i = 0; i < 15; ++i)
    {
        qint64 value = generator.generate() & std::numeric_limits<qint64>::max();
        std::cout << value << " ";
    }
    std::cout << std::endl;

    return a.exec();
}

Вывод будет следующим

Random Qt 3 - 853323747 2396352728 3025954838 2985633182 2815751046 340588426 3587208406 298087538 2912478009 3642122814 3202916223 799257577 1872145992 639469699 3201121432

По факту, здесь повторится та же проблема, что и у qrand , при многократном запуске программы вы увидите, что числа будут повторяться. В новости о выпуске Qt 5.10 сказано, что данный класс лучше функционирует, чем обычный qrand, но по факту проблема остаётся той же. Возможно при более длительном тестировании в рамках программы, которая постоянно использует генерацию случайных чисел можно увидеть существенные различия, но в рамках даже такого простого варианта уже заметны недостатки.

qrand

Будем генерировать числа в диапазоне значений от и до. Для этого напишем две функции.

static int randomBetween(int low, int high)
{
    return (qrand() % ((high + 1) - low) + low);
}

static int randomBetween(int low, int high, int seed)
{
    qsrand(seed); // Установка базового числа для отсчёта рандома в qrand
    return (qrand() % ((high + 1) - low) + low);
}

Первая функция просто генерирует случайное значение от наименьшего числа до наибольшего. Тогда как во второй с помощью функции qsrand устанавливается базовое число, которое служит основанием для генератора псевдослучайных числе Qt, от которого и генерируется число. Таким базовым числом может быть системное время в миллисекундах.

Применим данные функции.

#include <QCoreApplication>
#include <QDateTime>
#include <iostream>

static int randomBetween(int low, int high)
{
    return (qrand() % ((high + 1) - low) + low);
}

static int randomBetween(int low, int high, int seed)
{
    qsrand(seed); // Установка базового числа для отсчёта рандома в qrand
    return (qrand() % ((high + 1) - low) + low);
}

int main(int argc, char *argv[])
{
    QCoreApplication a(argc, argv);

    std::cout << "Random Qt 1 - ";
    for (int i = 0; i < 15; ++i)
    {
        std::cout << randomBetween(15, 43) << " ";
    }
    std::cout << std::endl;

    std::cout << "Random Qt 2 - ";
    for (int i = 0; i < 15; ++i)
    {
        std::cout << randomBetween(15, 43, QDateTime::currentMSecsSinceEpoch()) << " ";
    }
    std::cout << std::endl;

    return a.exec();
}

Получим следующий вывод.

Random Qt 1 - 15 21 31 27 17 34 43 33 22 32 30 34 35 38 31 
Random Qt 2 - 37 37 37 37 37 37 37 37 37 37 37 37 37 37 37

А теперь проанализируем полученный вывод.

В первом случае числа получились случайные… Но насколько? Если вы попробуете запустить программу несколько раз подряд, то увидите, что числа каждый раз будут одни и те же, что не очень хорошо и явно не очень случайно.

Что касается второго варианта, то здесь все числа получились одни и те же. Дело в том, что каждый раз мы пытались установить в качестве базового числа одни и то же число. Действительно, процессор с частотой в пару ГГц очень быстро выполнит тот простой цикл, а значит время в миллисекундах просто не успеет измениться, а значит и базовое число будет одинаковым. А при установке базового числа генерация будет производиться с самого начала и в данном случае вы увидите, что она не очень случайная.

А теперь посмотрим, что нам предложили в

Qt 5.10

Функция srand().

Да, каждый раз появляются одни и те же одинаковые числа. «Так себе генератор!» – скажете вы. И будете не совсем правы.
Действительно, генерируются всё время одинаковые числа. Но мы можем на это повлиять, для этого используется функция srand(), которая также определена в заголовочном файле stdlib.h. Она инициализирует генератор случайных чисел начальным числом.

Скомпилируйте и запустите несколько раз вот эту программу:

Листинг 5.

#include <stdio.h>
#include <stdlib.h>
 
int main(void) {
  srand(2);
/* генерируем пять случайных целых чисел из отрезка  */
  printf("%d\n", 80 + rand()%(100 - 80 + 1));
  printf("%d\n", 80 + rand()%(100 - 79));
  printf("%d\n", 80 + rand()%21);
  printf("%d\n", 80 + rand()%21);
  printf("%d\n", 80 + rand()%21);
}

Теперь поменяйте аргумент функции srand() на другое число (надеюсь вы ещё не забыли, что такое аргумент функции?) и снова скомпилируйте и запустите программу. Последовательность чисел должна измениться. Как только мы меняем аргумент в функции srand – меняется и последовательность. Не очень практично, не правда ли? Чтобы изменить последовательность, нужно перекомпилировать программу. Вот бы это число туда подставлялось автоматически.

И это можно сделать. Например, воспользуемся функцией time(), которая определена в заголовочном файле time.h.
Данная функция, если ей в качестве аргумента передать NULL, возвращает количество секунд, прошедших c 1 января 1970 года. Вот посмотрите, как это делается.

Листинг 6.

#include <stdio.h>
#include <stdlib.h>
#include <time.h> // чтобы использовать функцию time()
 
int main(void) {
  srand(time(NULL));
/* генерируем пять случайных целых чисел из отрезка  */
  printf("%d\n", 80 + rand()%(100 - 80 + 1));
  printf("%d\n", 80 + rand()%(100 - 79));
  printf("%d\n", 80 + rand()%21);
  printf("%d\n", 80 + rand()%21);
  printf("%d\n", 80 + rand()%21);
}

Вы спросите, а что такое NULL? Резонный вопрос. А я вам пока отвечу, что это специальное зарезервированное слово такое. Могу ещё сказать, что им обозначает нулевой указатель, но т.к. это для вас никакой информации не несёт, то на данный момент рекомендую об этом не думать. А просто запомнить как некоторый хитрый трюк. В будущих уроках мы остановимся на этой штуке поподробнее.

Вопрос 3. Псевдослучайные числа

Сложность: 3/3

Псевдослучайные числа — это, если очень упрощать, последовательность чисел, которая только выглядит случайной, а на самом деле каждое число в ней определяется алгоритмом, то есть вычисляется. Псевдослучайные последовательности цикличны: через какой-то период все числа повторяются в точности в том же порядке.

Библиотека random и модуль numpy.random содержат в себе генератор не истинно случайных, а именно псевдослучайных чисел.

Генерировать истинно случайные числа дорого и сложно. Основная трудность состоит в том, чтобы гарантировать отсутствие какого-либо цикла, правила или алгоритма. Чаще всего истинно случайные числа : шумов атмосферы, детекторов частиц, колебаний электрического тока или из космического излучения.

То, что псевдослучайная последовательность, в отличие от истинно случайной, воспроизводима, очень удобно для практических задач: часто нужно подать на вход ту же самую последовательность второй раз, чтобы посмотреть, как работает программа после добавления новых фич.

Визуализация работы генератора псевдослучайных чисел. Видите какую-нибудь закономерность? А она есть.Источник

Random.hpp

Класс, который реализован здесь использует синглетон Майерса, чтобы сделать статические методы получения случайных значений в определённом диапазоне. Гораздо же проще вызывать в нужном месте один статический метод класса, чем каждый раз предварительно инициализировать все генераторы случайных чисел. Сам класс работает как с целочисленными типами, так и типами значений с плавающей запятой.

#ifndef RANDOM_HPP
#define RANDOM_HPP

#include <random>

namespace details
{
    /// True if type T is applicable by a std::uniform_int_distribution
    template<class T>
    struct is_uniform_int {
        static constexpr bool value =
                std::is_same<T,              short>::value ||
                std::is_same<T,                int>::value ||
                std::is_same<T,               long>::value ||
                std::is_same<T,          long long>::value ||
                std::is_same<T,     unsigned short>::value ||
                std::is_same<T,       unsigned int>::value ||
                std::is_same<T,      unsigned long>::value ||
                std::is_same<T, unsigned long long>::value;
    };

    /// True if type T is applicable by a std::uniform_real_distribution
    template<class T>
    struct is_uniform_real {
        static constexpr bool value =
                std::is_same<T,       float>::value ||
                std::is_same<T,      double>::value ||
                std::is_same<T, long double>::value;
    };
}

class Random
{
    template <class T> using IntDist = std::uniform_int_distribution<T>;
    template <class T> using RealDist = std::uniform_real_distribution<T>;

public:
    template <class T>
    static typename std::enable_if<details::is_uniform_int<T>::value, T>::type get(T from = std::numeric_limits<T>::min(), T to = std::numeric_limits<T>::max())
    {
        if (from > to) std::swap(from, to);
        IntDist<T> dist{from, to};
        return dist(instance().engine());
    }

    template <class T>
    static typename std::enable_if<details::is_uniform_real<T>::value, T>::type get(T from = std::numeric_limits<T>::min(), T to = std::numeric_limits<T>::max())
    {
        if (from > to) std::swap(from, to);
        RealDist<T> dist{from, to};
        return dist(instance().engine());
    }

    std::mt19937& engine() { return m_mt; }

protected:
    static Random& instance()
    {
        static Random inst;
        return inst;
    }

private:
    std::random_device m_rd; // Устройство генерации случайных чисел
    std::mt19937 m_mt;       // Стандартный генератор случайных чисел

    Random() : m_mt(m_rd()) {}
    ~Random() {}
    Random(const Random&) = delete;
    Random& operator = (const Random&) = delete;
};

#endif // RANDOM_HPP

Инициализация генератора и seed

Этап объявления, определения и создания сущностей зачастую рассматривается как нечто, не стоящее особого внимания. Но недостаточно вдумчивая инициализация генератора случайных чисел может сказаться на его надлежащей работе.

Первые 2 инициализации эквивалентны. И по большей части имеют отношение к вкусу или к стандартам написания красивого кода. А вот следующая инициализация в корне отличается.

«31255» — это называется seed (семя, первоисточник) — число, на основе которого генератор создает случайные числа. Ключевым моментом здесь является то, что при такой инициализации тип seed должен быть таким же или приводимым к типу, с которым работает генератор. Этот тип доступен через конструкцию decltype(e()), или result_of, или typename.

Распределения

Сами по себе, генераторы, конечно, незаменимы, но без возможности указания диапазона нужного значения они становятся лишь чуть лучше, чем srand. Я рассмотрю два основных распределения, но их существует гораздо большее количество, на все случаи жизни, так сказать.

Все они принимают в качестве аргументов в конструкторе либо параметры другого распределения, либо переменные, отвечающие за диапазон значений. Если оные не указаны, то используется диапазон от 0 до максимального значения, определенного в numeric_limits<>::max() данного идентификатора типа, являющегося параметром шаблона.

Если указан лишь один аргумент, то берется диапазон значений от данного до максимального. Следует отметить, что границы также учитываются, т.е. при указании в качестве аргументов a, b используется диапазон .

Оператор () принимает в качестве параметра генератор и возвращает число из диапазона распределения. При этом на одно и то же распределение можно применять совершенно различные генераторы, отвечают они лишь за диапазон.

Функции для получения целых «случайных» чисел – randint() и randrange()

Функции и генерируют псевдослучайные целые числа. Первая из них наиболее простая и всегда принимает только два аргумента – пределы целочисленного диапазона, из которого выбирается любое число:

>>> random.randint(0, 10)
6

или (если импортировались отдельные функции):

>>> randint(100, 200)
110

В случае обе границы включаются в диапазон, т. е. на языке математики отрезок описывается как .

Числа могут быть отрицательными:

>>> random.randint(-100, 10)
-83
>>> random.randint(-100, -10)
-38

Но первое число всегда должно быть меньше или, по-крайней мере, равно второму. То есть a <= b.

Функция сложнее. Она может принимать один аргумент, два или даже три. Если указан только один, то она возвращает случайное число от 0 до указанного аргумента. Причем сам аргумент в диапазон не входит. На языке математики – это [0; a).

>>> random.randrange(10)
4

Или:

>>> randrange(5)
0

Если в передается два аргумента, то она работает аналогично за одним исключением. Верхняя граница не входит в диапазон, т. е. [a; b).

>>> random.randrange(5, 10)
9
>>> random.randrange(1, 2)
1

Здесь результатом второго вызова всегда будет число 1.

Если в передается три аргумента, то первые два – это границы диапазона, как в случае с двумя аргументами, а третий – так называемый шаг. Если, например, функция вызывается как , то «случайное» число будет выбираться из чисел 10, 13, 16, 19:

>>> random.randrange(10, 20, 3)
13
>>> random.randrange(10, 20, 3)
19
>>> random.randrange(10, 20, 3)
10

Случайности не случайны

Так говорил мастер Угвэй, и мы теперь понимаем его чуть лучше: он жил довольно долго, мог заметить период повторения одних и тех же событий и догадаться, что все случайности в этом мире на самом деле псевдослучайны. У нас с вами времени меньше, поэтому придётся изучать документацию: random, numpy.random.

А чтобы никакая псевдослучайность не помешала вам успешно пройти собеседование, приходите в наш Шаолинь на курс «Профессия Python-разработчик». Вы изучите random, numpy и ещё много приёмов пайтонического кунг-фу, а мы поможем с наставниками, единомышленниками и, конечно, с трудоустройством.