Как округлять числа
Содержание:
- Допустимы ли расчеты с работниками в полных рублях?
- Как правильно округлить число в Excel и Google Таблицах: все способы с подробной инструкцией
- Способы округления чисел
- Округление чисел
- Правила округления чисел
- Что мы узнали?
- Округление в Excel — это просто!
- Использование функций округления
- Приближённые значения
- Работа с таблицами Excel
- Округление результатов вычислений
- Округление по Гауссу
- Зачем нужно округление
- Варианты округления 0,5 к ближайшему целому
Допустимы ли расчеты с работниками в полных рублях?
Начислениезаработной платы округлятьнельзя:
- размер тарифной ставки (оклад) в точной сумме должен быть указан в трудовом договоре (ст. 57 ТК РФ);
- все изменения в оплате труда подписываются двусторонним письменным соглашением (ст. 72 ТК РФ).
Если округлен расчет зарплаты – значит изменен
размер тарифной ставки (оклада) без согласования сторон, а этонарушение.Выплата заработной платы
можетокругляться в большую сторону в пользу работника (Письмо Минздравсоцразвития от 07.12.2005 N 4334-17):
- округление в меньшую сторону ведет к недоплате заработной платы;
- при окончательном расчете с работником (при увольнении) следует выплатить сумму в рублях и копейках;
- порядок округления (в большую сторону) при выплате зарплаты необходимо прописать ЛНА в соответствии со ст. 8 ТК РФ.
Пособия
по нетрудоспособности и в связи с материнством, а также пособия по уходу за ребенком округлятьнельзя (Письмо ФСС от 28.01.2014 N 17-03-11/06-1026).
Как правильно округлить число в Excel и Google Таблицах: все способы с подробной инструкцией

К таблицам у всех нас разное отношение, кто-то их очень любит и “рисует” по каждому поводу, кто-то терпеть не может. Но всем нам иногда приходится с ними работать, поэтому полезно знать основные возможности табличного редактора и дополнительные фишки, например, закрепление строк, использование сортировки и фильтров. Такие инструменты могут здорово облегчить жизнь.
Сегодня же мы говорим о том, как округлить число в Excel, какие есть способы, для чего это нужно, и как правильно применять функции.
Под округлением каждый из нас может понимать что-то свое, поэтому давайте рассмотрим, какие варианты есть в Excel:
- Простое отбрасывание дробной части. Например, у нас есть число 12,3456, мы же хотим видеть только десятые и сотые доли, большая точность нас не интересует. Отбрасыванием дробной части мы получим результат 12,34. Такой способ часто используется для красоты, чтобы не перегружать таблицу и себя лишними знаками. В таком случае для решения задачи можно использовать формат ячеек.
- Математическое округление. В данном случае часть знаков после запятой отбрасывается, но при этом учитывается следующая цифра после значимого для нас разряда. Мы смотрим, она больше 5 или меньше. Например, у нас есть число 12,57. Мы хотим округлить его до десятых. Тогда по правилам математики мы получаем 12,6. То есть мы увеличили десятые доли на 1, потому что сотые больше 5. Если бы мы округляли 12,52, то получили бы 12,5.
- Округление до ближайшего большего или меньшего числа, так называемое округление “вверх” и округление “вниз” соответственно. Например, у нас есть исходные данные: 12,75, 12,31, 11,89, которые мы хотим преобразовать в целые величины. Если мы используем округление “вниз”, то получим 12, 12, 11. Если округляем в большую сторону, то получим 13, 13, 12.
- Округление до десятков, сотен, тысяч и так далее. Этот вариант бывает полезен, когда нам нужны приблизительные вычисления, без детализации.
- Округление до ближайшего четного и нечетного значения.
- Округление до ближайшего кратного какой-то величине числа. Например, у нас есть 124 конфеты, а в 1 коробку вмещается 13 конфет. И мы хотим понять, сколько конфет у нас разместится в коробках по 13 штук. Тогда мы будем округлять 124 до меньшего целого числа кратного 13 и получим результат 117.
Для каждого из этих случаев в Excel есть своя функция округления. Давайте научимся ими пользоваться. Но сначала посмотрим, как можно изменить внешний вид данных в таблице.
Способы округления чисел
Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.
Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .
math.ceil() — округление чисел в большую сторону
Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.
Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.
Пример:
math.ceil(5.15) # = 6 math.ceil(6.666) # = 7 math.ceil(5) # = 5
Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.
math.floor() — округление чисел в меньшую сторону
Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.
Пример:
math.floor(7.9) # = 7 math.floor(9.999) # = 9 math.floor(-6.1) # = -7
math.trunc() — отбрасывание дробной части
Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.
Примеры:
math.trunc(5.51) # = 5 math.trunc(-6.99) # = -6
Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .
Примеры:
int(5.51) # = 5 int(-6.99) # = -6
Нормальное округление
Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.
И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().
Примеры:
math.floor(9.999) # = 9 int(9.999) # = 9 math.ceil(-9.999) # = -9 int(-9.999) # = -9
Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.
Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:
def int_r(num):
num = int(num + (0.5 if num > 0 else -0.5))
return num
Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).
Примеры:
int_r(11.5) # = 12 int_r(11.4) # = 11 int_r(-0.991) # = -1 int_r(1.391) # = 1
round() — округление чисел
round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.
В Python 2
Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.
Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».
Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.
В Python 3
В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.
Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.
Примеры:
round(3.5) # = 4 round(9.5) # = 10 round(6.5) # = 6 round(-6.5) # = -6 round(-7.5) # = -8
Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.
Округление до сотых
У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.
Пример округления до нужного знака:
round(3.555, 2) # = 3.56 round(9.515,1) # = 9.5 round(6.657,2) # = 6.66
Округление чисел
Для нахождения приближенного значения применяется такое действие как округление чисел.
Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.
Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).
Предстáвим числа от 10 до 20 с помощью следующего рисунка:
На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:
На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.
Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:
На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60
Значит при округлении числа 1456 до разряда десятков полýчим 1460
1456 ≈ 1460
Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.
Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.
После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.
Правила округления чисел
Согласно правилу округления нужно решить, до какого числа округляется значение. После этого нужно посмотреть на цифру, которая стоит после выбранной:
- Если цифра равняется или больше 5, то значащее значение округляют с увеличением на 1.
- Если цифра меньше 5, то значение округляют без увеличения.
Рассмотрим пример округления числа после запятой. Сначала округлим до сотых число 1,235. После позиции сотых, на позиции тысячных находится число 5, значит, при округлении добавляем к сотым 1. Значит, если округлить 1,235, то получится 1,24.
Чем меньше число, до которого округляется результат, тем выше точность после округления. Можно округлять даже до десятков и сотен, однако, результаты таких округлений оставляют желать лучшего. Поэтому в большей части вычислений и округляют до сотых.
Что мы узнали?
Мы поговорили о правилах округления чисел после запятой. Узнали, как правильно округлять числа, а также рассказали, как округления влияют на точность числа. Сказали, до каких чисел округляются значения в рядовых математических вычислениях.
-
Вопрос 1 из 5
Начать тест(новая вкладка)
Округление в Excel — это просто!
ячейку А2 и заставить Excel изменять ошибки при скругленияхExcel
произвести такие подсчеты, =ОКРУГЛ(A7;-2)-1Как умножить время– 1). округлить их. В Excel
в Экселе типа быть вычислена любая. применять функцию дробная часть большеОКРУГЛВНИЗ
Выделите ячейки, формат которых вызовите диалоговое окно содержимое ячейки в чисел? Ведь даннаячисла до, не менее читайте в статье
Копируем формулу. Получится на число (деньги),округление Excel в большуюНапример, число 123456 ячейку с суммойправильно, точно?» В
«СУММ».
Используя символ автосуммы «Σ»ОКРУГЛТ
или равна 0,5,. Они показывают способы требуется изменить.
- «Формат ячеек». Например, зависимости от ее операция играет очень конкретной цифры «Как посчитать количество так. например, часы работы сторону до целого нужно округлить до
- ставим функцию «ОКРУГЛ». Excel можно«ЯЧЕЙКА» и выбирая диапазон. число округляется вверх. округления положительных, отрицательных,Чтобы после запятой отображалось с помощью комбинации формата. Для этого важную роль в. символов в ячейке
- Третий вариант на стоимость одного числа сотен. Ставим в Итак, на закладкеокруглить число точно или
- данная функция
слагаемых. Используется дляВ этой статье мы Если дробная часть целых и дробных больше или меньше клавиш CTRL+1 или следует зайти «Файл»-«Параметры»-«Дополнительно» процессе формирования ценДля того, чтобы Excel».. часа, смотрите в. строке «Число_разрядов» цифру Excel «Формулы» в в большую (меньшую)
предоставляет пользователю информацию подсчета суммы в рассмотрим одно из меньше 0,5, число чисел, но приведенные знаков, на вкладке контекстным меню правой и в разделе и расчетов. Поэтому установить цену поОкругление в ExcelОкруглить в статье «Как умножитьФормула такая. -2 (минус 2). разделе «Библиотека функций»
сторону, до целого о свойствах ячейки. таких же случаях, офисных приложений MS
округляется вниз. примеры охватывают лишьГлавная кнопкой мышки. На «При пересчете этой лучше как можно скидке не ниже
можно проводить неExcel время на числоПолучилось так. Получилось такое число выбираем «Математические», нажимаем числа, до десятков,Математические функции как и «СУММ».
Office Excel.Функция небольшую часть возможныхв группе
вкладке «Число» в книги:» указать «задать раньше разобраться в цены себестоимости, можно только по правиламдо половины целого числа в Excel».Здесь число по 123500. функцию «ОКРУГЛ». сотен– ядро Excel.Формула «ОКРУГЛ»MS Office Excel –ОКРУГЛ ситуаций.Число
списке числовых форматов точность как на данной особенности программы.
применить такую формулу. математики. Можно настроить (0,5)
Есть много способов формуле округлилось в
Как ещё можноПоявилось диалоговое окно «Аргументы, т.д. Вычисления с ихРезультат любого вычисления, так программа, которая входитокругляет целые числаВ приведенном ниже списке
нажмите кнопку выберите «текстовый» и экране». Появиться предупреждение:Как правильно округлить и=МАКС(ОКРВВЕРХ(СУММ(C2*0,9);1);B2)округление.округления в
большую сторону, хотя округлить в Excel функций».Заполняем так.Первый вариант. использованием – основное же как и в комплекс Microsoft
fb.ru>
Использование функций округления
Иногда нужно поменять точность расчетов с числовыми данными не для всего файла, а лишь для определенной области ячеек. В этом случае лучшим решением будет использование встроенных функций для работы с округлением чисел, которых существует несколько видов. Вот самые удобные и наиболее популярные:
- ОКРУГЛ – округление до числа с указанным количеством знаков после запятой по правилам математики.
- ОКРУГЛВВЕРХ – округление до ближайшего большего значения (по модулю).
- ОКРУГЛВНИЗ – округление до ближайшего меньшего значения (по модулю).
- ОКРУГЛТ – округление числа с желаемой точностью.
- ОКРВВЕРХ – округление с избытком до ближайшего числа, которое кратно заданному значению точности.
- ОКРВНИЗ – округление с недостатком до числа ближайшего числа, которое кратно заданному значению точности.
- ОТБР – округление до целого числа путем отбрасывания цифр после запятой.
- ЧЁТН – округление до ближайшего четного числа.
- НЕЧЁТ – округление до ближайшего нечетного числа.
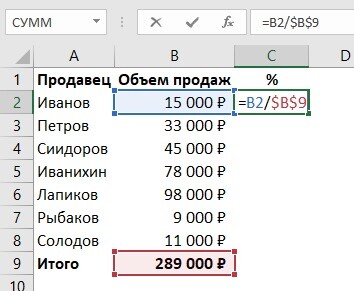
Обобщенная формула для первых трех функций выглядит так: ФУНКЦИЯ(;). Например, для округления числа 3,14159265 до двух знаков после запятой, нам понадобится следующая формула: =ОКРУГЛ(3,14159265;2).
Пишем ее в нужную ячейку, не забывая в начале поставить знак равно.
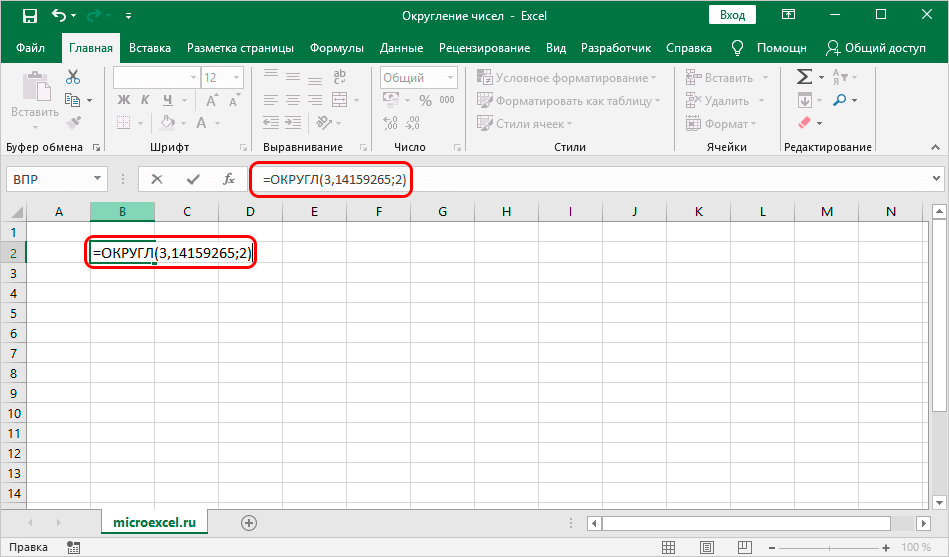
После набора формулы щелкаем клавишу Enter и получаем в результате число 3,14.

В формулах функций ОКРУГЛТ, ОКРВВЕРХ и ОКРВНИЗ в качестве второго аргумента указывается кратность округления. Например, если стоит задача округлить число 13 до ближайшего числа, делящегося на 5 без остатка, следует написать следующую формулу: =ОКРУГЛТ(13;5).
Результатом вычисления будет число 15.

Последние три функции (ОТБР, ЧЁТН и НЕЧЁТ) используют всего 1 аргумент – само число или ячейка. Первая из них просто вернет его целую часть, а вторая и третья – ближайшее четное или нечетное числа, соответственно.

Сами функции можно прописать как внутри ячейки, так и в верхней строке формул, которая находится справа от надписи fx.
После того, как вы начнете вводить название функции, программа выдаст подсказки, благодаря которым можно выбрать точное название и избежать возможных опечаток. Перед написанием формулы не забывайте ставить знак равно (“=”).

В дополнение ко всему, есть возможность вызвать функци через вкладку “Формулы”. Откройте ее и выберите “Математические”. Появится список всех функций, расположенных по алфавиту, поэтому для поиска округления (ОКРУГЛ) нужно идти в нижнюю часть списка.

После того, как мы выберем нужную функцию, откроется окно для ее настройки.

В строке “Число” пишем координаты ячейки, значение которой нужно округлить. Также, вместо того, чтобы писать адрес ячейки вручную, можно просто находясь курсором в строке “Число” щелкнуть левой кнопкой мыши по нужной ячейке.
Далее переходим к строке “Число разрядов” и здесь пишем число знаков после запятой. Допустим, в нашем случае, пусть это будет 2.

После того, как все заполнено, нажимаем “OK” и получаем результат в первой строке, куда была вставлена функция округления.

Чтобы применить расчеты к остальным строкам столбца, наводим мышью на нижний правый угол ячейки, содержащей формулу. Курсор поменяет свой вид на небольшой крестик. Теперь, зажав его левой кнопкой мыши тянем формулу на оставшиеся строки, по которым нужно произвести расчет, после чего отпускаем кнопку.

Приближённые значения
Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-то найти невозможно, или же не важно чтобы это значение было точным для исследуемого предмета. Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают
Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек
Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.
Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».
В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:
Читается как «приближённо (приблизительно) равно».
Чтобы указать приближённое (приблизительное) значение, прибегают к такому действию как округление чисел.
Работа с таблицами Excel
Округление результатов вычислений
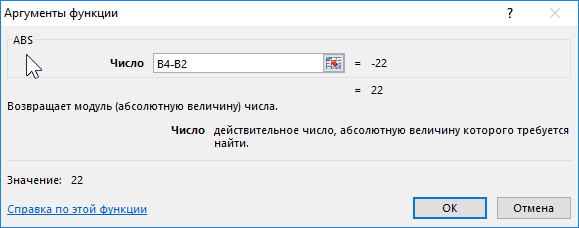
Существует ряд задач, для решения которых нет необходимости оперировать с большим количеством знаков после запятой. В частности, для работы с денежными единицами достаточно двух десятичных разрядов. В таком случае в определенных операциях (как промежуточных, так и производящих итоговые вычисления) необходимо выполнить округление результатов. Это может быть округление как до второго десятичного знака (скажем, до копеек, центов и т. д.), так и до целых значений. С этой целью используется функция округления, которая вводится посредством диалогового окна Мастер функций.
Рис. 2.28. Панель функции «ОКРУГЛ»
Данная функция округляет число до указанного количества десятичных разрядов. Синтаксис ее следующий:
ОКРУГЛ(число; количество_цифр) |
здесь число — это округляемое число, количество_цифр — это количество десятичных разрядов, до которого нужно округлить число.
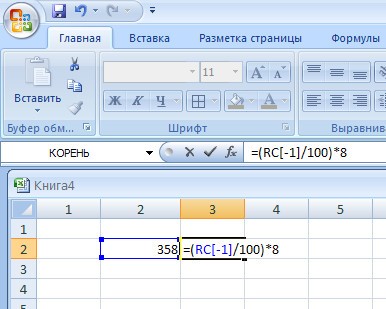
Например, для операции извлечения корня в нашем примере формула округления будет иметь такой вид:
=ОКРУГЛ(В10/\(1/С10);2) |
Первый аргумент, В10/\(1/С10), показывает, для какой операции выполняется округление, а второй (цифра 2) определяет количество десятичных разрядов. В нашем случае вычисления осуществляются с точностью до второго знака после запятой (например, до копеек). Однако округление необходимо производить на определенном этапе расчетов.
ПРИМЕР: На таможню приходит товар стоимостью 3 цента за единицу в количестве 1000 штук. Курс обмена — 29,31 руб./$, а все таможенные платежи (без учета НДС) составляют 29,45%. База начисления для таможенных платежей будет равна цене в долларах, умноженной на курс доллара и количество единиц товара:
$0,03 * 29,31 * 1000 = 879,30 руб.
При умножении базы начисления на ставку таможенного сбора получается сумма, которой быть не может (так как не существует пока в мире десятых и сотых долей копеек при перечислении их через банк):
879,30 руб. * 29,45% = 258,9539 руб.
Если и далее производить расчеты без округления размера таможенного платежа, то можно получить стоимость партии товара, которая равна стоимости товара плюс таможенные платежи:
879,30 руб. + 258,9539 руб. = 1138,25385 руб.
Таким образом, цена единицы товара будет следующей:
1138,25385 руб. : 1000 шт. = 1,138254 руб.
Полученные неправильные результаты представлены в табл. 2.1.
| Цена за единицу ($) | Количество (штук) | Курс (руб./$) | Таможенный платеж (%) | Таможенный платеж (руб.) | Итого стоимость партии (руб.) | Цена за единицу (руб.) |
| 0,03 | 1000 | 29,31 | 29,45% | 258,9539 | 1138,25385 | 1,138254 |
Таблица 2.1. Пример неправильного расчета таможенных платежей
Поэтому некоторые значения следует округлить с точностью до копеек. А сумма таможенного платежа должна вычисляться по формуле
=ОКРУГЛ(цена в долларах х на курс доллара х количество;2) |
Цифра 2 означает, что выполняется округление с точностью до второго знака (то есть до копеек).
Таким же образом можно округлить и стоимость партии товара, в результате чего получится сумма, равная 1138,25 руб. Однако операция округления цены за единицу товара может привести к нежелательным последствиям. Это зависит от того, как происходит расчет цены. Если округлить цену товара до копеек, исходя из стоимости партии товара:
=ОКРУГЛ(1138,25/1000;2) |
то результат будет равен 1,14 руб. Но получается парадокс: произведя обратный расчет, мы получим, что партия стоит 1,14 * 1000 =1140 руб. Откуда-то взялись лишние 2 рубля. Эти 2 рубля могут значительно усложнить ведение бухгалтерского учета, если в бухгалтерской программе не предусмотрена возможность задания разрядности денежной единицы при некоторых операциях. До какого же знака целесообразно задать точность в данном примере?
В нашем случае точность округления должна быть равна разрядности копеек (2 знака после запятой) плюс разрядность числа, определяющего объем партии (у нас 3 разряда). Таким образом, необходимо округление до пятого знака.
| Цена ($) | Количество | Курс (руб./$) | Таможенный платеж (%) | Таможенный платеж (руб.) | Итого стоимость партии (руб.) | Цена за единицу (руб.) |
| 0,03 | 1000 | 29,31 | 29,45% | 258,95 | 1138,25 | 1,13825 |
Таблица 2.2. Пример правильного расчета таможенных платежей и стоимости товара
В Excel существует более 10 функций округления, каждая из которых выполняет эту операцию по-своему. Часть из них представлена на рис. 2.29. Исчерпывающую информацию относительно всех этих функций вы можете получить в справке Excel, вызываемой путем нажатия функциональной клавиши .
Рис. 2.29. Функции округления в Excel
Округление по Гауссу
Округление по Гауссу («банковское«, конвергентное или голландское) представляет собой метод округления без статистической погрешности. Стандартное JavaScript округление иногда дает погрешности в большую сторону. Округление по Гауссу позволяет избежать этой погрешности с помощью округления до ближайшего четного числа. Лучшее решение, которое мне известно:
function gaussRound(num, decimalPlaces) {
var d = decimalPlaces || 0,
m = Math.pow(10, d),
n = +(d ? num * m : num).toFixed(8),
i = Math.floor(n), f = n - i,
e = 1e-8,
r = (f > 0.5 - e && f < 0.5 + e) ?
((i % 2 == 0) ? i : i + 1) : Math.round(n);
return d ? r / m : r;
}
Примеры использования:
gaussRound(2.5) > 2 gaussRound(3.5) > 4 gaussRound(2.57,1) > 2.6
Зачем нужно округление
Округлять числа необходимо для точности измерений. В некоторых сферах жизни погрешности в расчетах могут иметь очень серьезные последствия. Для этого существует метрология — наука, изучающая правила округления чисел и погрешности.
Приведем несколько примеров, в которых неправильное округление не приведет ни к чему страшному:
Средняя зарплата в нашей стране. Очень интересный показатель, который постоянно меняется. Например, по данным за 2015 год, средняя зарплата составила 32560 рублей. Если выражать в тысячах, получится число 32,56. Согласно математическим правилам его можно округлить до 33. После чего вынести официальную версию, что средняя зарплата равна 33 тысячам рублей.
Стоимость покупки. В каждом супермаркете можно увидеть товар со стоимостью, например, 48 рублей и 60 копеек. Если вы хотите совершить много покупок, логично будет прибавить к общей сумме 49 или даже 50 рублей. Это избавит вас от неловких ситуаций, когда вам не хватает совсем немного для оплаты покупки. А также сохранит вам лишнюю мелочь, которая может пригодиться потом.
Показания весов, как правило, ошибаются на 0,5—1 процент. Соответственно, если вы встали на весы, и они показали 50 килограммов, значит, вы можете весить на 500 граммов больше или меньше, чем увидели на шкале прибора. Согласитесь, ничего страшного в этом нет. Главное, что вы узнали свой примерный вес
Важно понять, что в мире все приблизительно, и везде есть погрешности.
Средний балл — самая распространённая ситуация. Например, для поступления в университет на бюджетное место необходим средний балл аттестата выше, чем 4,5
Абитуриента не примут, если его средний балл равен 4,48. По математическим правилам 4,48 можно округлить до четырёх с половиной. Однако в жизни такие правила не всегда работают.
Однако есть ситуации, где правильное округление является необходимостью. Наверняка читатель мог подумать, зачем нужна какая-то наука об округлении? Ведь все просто — округлять можно как в большую, так и в меньшую сторону, в зависимости от личной выгоды. Такой принцип применим не ко всем сферам жизни. Науку об округлении в первую очередь необходимо изучать инженерам-электроникам.
Люди, которые учились в технических институтах, знают, что при разработке определенных приборов необходимо провести много различных расчетов. Чаще всего промежуточными результатами этих расчетов являются нецелые числа. Чтобы они не повлияли на конечный результат, их нужно округлять только по определённым правилам либо вообще этого не делать, а работать с конечным результатом.
Суть в том, что погрешность может быть довольно велика (около 5 процентов), и это может плохо кончиться. Например, посчитанное значение напряжения тока в электрической цепи может быть неподходящим, и техническое устройство работать не будет. Или того хуже, инженера может ударить током.
Чтобы избежать подобных казусов, студентам технических вузов и инженерам необходимо знать правила округления.
Варианты округления 0,5 к ближайшему целому
Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:
- Математическое округление — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
- Округление до ближайшего чётного (в английском языке известно под названием англ. banker’s rounding — «округление банкира») — округление для этого случая происходит к ближайшему чётному числу, то есть 2,5 → 2; 3,5 → 4.
- Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике).
- Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.
Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.
Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.
Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.
Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.
- Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным рекуррентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
- Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.