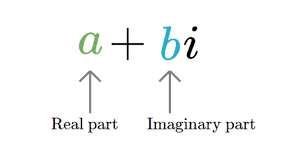Установка и первое знакомство

Check if NumPy array is empty

We can use the size method which returns the total number of elements in the array.

In the following example, we have an if statement that checks if there are elements in the array by using ndarray.size where ndarray is any given NumPy array:

import numpy

a = numpy.array()

if(a.size == 0):

    print("The given Array is empty")

else:

    print("The array = ", a)

The output is as follows:

In the above code, there are three elements, so it’s not empty and the condition will return false.

If there are no elements, the if condition will become true and it will print the empty message.

If our array is equal to:

a = numpy.array([])

The output of the above code will be as below:

Пример функции Numpy cumsum ()?

Здесь мы обсудим, как мы можем написать функцию cumsum() из библиотеки numpy.

1. Принимая в качестве входных данных только переменную

В этом примере мы импортируем библиотеку numpy в python. Мы не будем принимать входные данные в виде массива. Мы возьмем целочисленную переменную, а затем применим функцию numpy cumsum () . Следовательно, мы увидим, что преобразование сделано. Давайте рассмотрим этот пример для более детального понимания концепции.

#taking input as a variable
#importing numpy library
import numpy as np

a = 15
print("input taken : ",a)
output = np.cumsum(a)
print("conversion done : ",output)

Выход:

input taken :  15
conversion done :  

Объяснение:

• Во-первых, мы будем импортировать библиотеку numpy с псевдонимом np.
• Затем мы возьмем переменную a, в которой хранится целочисленное значение 15.
• После этого мы напечатаем входное значение.
• Затем мы применим функцию numpy cumsum() и сохраним выходные данные в выходной переменной.
• Наконец, мы напечатаем результат.
• Следовательно, вы можете видеть результат как выполненное преобразование, так как это было единственное целочисленное значение.

2. Принятие входных данных в виде массива

В этом примере мы импортируем модуль numpy. Затем мы будем принимать входные данные в виде массива, а затем применять функцию numpy cumsum () . Наконец, мы увидим совокупную сумму массива. Давайте рассмотрим этот пример для более детального понимания концепции.

#taking input as an array
#importing numpy library
import numpy as np

arr = np.array(, ])
print("input taken : ",arr)
output = np.cumsum(arr)
print("Cumulative sum of array : ",output)

Выход:

input taken :  
 ]
Cumulative sum of array :  

Объяснение:

• Во-первых, мы будем импортировать библиотеку numpy с псевдонимом np.
• Затем мы будем принимать входные данные в виде массива, внутри которого есть несколько целочисленных значений.
• После этого мы напечатаем входной массив.
• Затем мы применим функцию numpy cumsum() и сохраним выходные данные в выходной переменной.
• Наконец, мы напечатаем результат.
• Следовательно, вы можете видеть результат как совокупную сумму массива.

3. Взятие массива и оси в качестве параметра

В этом примере мы импортируем модуль numpy. Затем мы будем принимать входные данные в виде массива и применять ось как 0 и 1 в качестве параметра . Наконец, мы увидим выход на обеих осях и увидим разницу. Давайте рассмотрим этот пример для более детального понимания концепции.

#taking input as an array and axis parameter
#importing numpy library
import numpy as np

arr = np.array(, ])
print("input taken : ",arr)
output = np.cumsum(arr, axis = 0)
print("Cumulative sum of array at axis = 0: ",output)
out = np.cumsum(arr, axis = 1)
print("Cumulative sum of array at axis = 1 : ",out)

Выход:

input taken :  
 ]
Cumulative sum of array at axis = 0:  
 ]
Cumulative sum of array at axis = 1 :  
 ]

Объяснение:

• Во-первых, мы будем импортировать библиотеку numpy с именем as np.
• Затем мы будем принимать входные данные в виде массива, внутри которого есть несколько целочисленных значений.
• После этого мы напечатаем входной массив.
• Затем мы применим функцию numpy cumsum() с массивом, а ось будет равна 0 и 1 и сохранит выходные данные в переменной output и out.
• Наконец, мы напечатаем оба вывода.
• Следовательно, вы можете видеть результат как совокупную сумму массива с и.

4. Взятие массива и типа d в качестве параметра

В этом примере мы импортируем модуль numpy. Тогда мы будем принимать входные данные как массив и как тип данных массива. Наконец-то мы увидим результат. Давайте рассмотрим этот пример для более детального понимания концепции.

#taking input as an array and dtype as a parameter
#importing numpy library
import numpy as np

arr = np.array(, ])
print("input taken : ",arr)
output = np.cumsum(arr, dtype = float)
print("Cumulative sum of array : ",output)

Выход:

input taken :  
 ]
Cumulative sum of array :  

Объяснение:

• Во-первых, мы будем импортировать библиотеку numpy с псевдонимом np.
• Затем мы будем принимать входные данные в виде массива, внутри которого есть несколько целочисленных значений.
• После этого мы напечатаем входной массив.
• Затем мы применим функцию numpy cumsum() с массивом и в качестве параметра и сохраним выходные данные в выходной переменной.
• Наконец, мы напечатаем результат.
• Следовательно, вы можете видеть выходные данные как совокупную сумму массива в типе данных float.

1.4.1.6. Copies and views¶

A slicing operation creates a view on the original array, which is
just a way of accessing array data. Thus the original array is not
copied in memory. You can use to check if two arrays
share the same memory block. Note however, that this uses heuristics and may
give you false positives.

When modifying the view, the original array is modified as well:

>>> a = np.arange(10)
>>> a
array()
>>> b = a)
>>> np.may_share_memory(a, b)
True
>>> b = 12
>>> b
array()
>>> a   # (!)
array()

>>> a = np.arange(10)
>>> c = a)

>>> np.may_share_memory(a, c)
False

This behavior can be surprising at first sight… but it allows to save both
memory and time.

Параметры стандартного отклонения Numpy

• a: array_like – этот параметр используется для вычисления стандартного отклонения элементов массива.
• ось: None, int или кортеж ints – Вычисление стандартного отклонения необязательно. В этом случае мы определяем ось, вдоль которой вычисляется стандартное отклонение. По умолчанию он вычисляет стандартное отклонение сплющенного массива. Если у нас есть кортеж ints, стандартное отклонение выполняется по нескольким осям, а не по одной оси или всем осям, как раньше.
• dtype: data_type – Он также необязателен при расчете стандартного отклонения. По умолчанию для массивов целочисленного типа используется тип данных float64, а массив типа float будет точно таким же, как и тип массива.
• out: ndarray – Это также необязательно при расчете стандартного отклонения. Этот параметр используется в качестве альтернативного выходного массива, в который должен быть помещен результат. Он должен иметь ту же форму, что и ожидаемый результат, но при необходимости мы можем его напечатать.
• ddof: int – Это также необязательно при расчете стандартного отклонения. Это определяет дельта-степень свободы. Делитель, который используется в вычислениях, равен N-ddof, где N представляет количество элементов. По умолчанию ddof равен нулю.
• keepdims: bool – Это необязательно. Когда значение равно true, оно оставит уменьшенную ось в виде размеров с размером один в результирующей. Когда передается значение по умолчанию, оно позволяет нестандартным значениям проходить через метод mean подклассов ndarray, но keepdims не проходят.

Сортировка, поиск, подсчет¶

Команда	Описание
sort(a)	отсортированная копия массива
lexsort(keys)	Perform an indirect sort using a sequence of keys.
argsort(a)	аргументы, которые упорядочивают массив
array.sort()	сортирует массив на месте (метод массива)
msort(a)	копия массива отсортированная по первой оси
sort_complex(a)	сортировка комплексного массива по действительной части, потом по мнимой
argmax(a)	индексы максимальных значений вдоль оси
nanargmax(a)	индексы максимальных значений вдоль оси (игнорируются NaN).
argmin(a)	индексы минимальных значений вдоль оси
nanargmin(a)	индексы минимальных значений вдоль оси (игнорируются NaN).
argwhere(a)	массив индексов ненулевых элементов. данные сгруппированы по элементам(,….)
nonzero(a)	массивы индексов ненулевых элементов. сгруппированы по размерностям (индексы X, индексы Y, т.д.)
flatnonzero(a)	индексы ненулевых элементов в плоской версии массива
where(condition, )	возвращает массив составленный из элементов x (если выполнено условие) и y (в противном случае). Если задано только condition, то выдает его «не нули».
searchsorted(a, v)	индексы мест, в которые нужно вставить элементы вектора для сохранения упорядоченности массива
extract(condition, a)	возвращает элементы (одномерный массив), по маске (condition)
count_nonzero(a)	число ненулевых элементов в массиве

Multi-dimensional Array:

a=np.array()print(a)Output -           ]

Many of you must be wondering that why do we use python numpy if we already have python list? So, let us understand with some examples in this python numpy tutorial.

Python NumPy Array v/s List

We use python numpy array instead of a list because of the below three reasons:

1. Less Memory
2. Fast
3. Convenient

The very first reason to choose python numpy array is that it occupies less memory as compared to list. Then, it is pretty fast in terms of execution and at the same time, it is very convenient to work with. So these are the major advantages that python numpy array has over list. Don’t worry, I am going to prove the above points one by one practically in PyCharm. Consider the below example:

import numpy as npimport timeimport sysS= range(1000)print(sys.getsizeof(5)*len(S)) D= np.arange(1000)print(D.size*D.itemsize)Output -  14000          4000

The above output shows that the memory allocated by list (denoted by S) is 14000 whereas the memory allocated by the numpy array is just 4000. From this, you can conclude that there is a major difference between the two and this makes python numpy array as the preferred choice over list.

Next, let’s talk how python numpy array is faster and more convenient when compared to list.

import timeimport sysSIZE = 1000000L1= range(SIZE)L2= range(SIZE)A1= np.arange(SIZE)A2=np.arange(SIZE)start= time.time()result=print((time.time()-start)*1000)start=time.time()result= A1+A2print((time.time()-start)*1000)Output - 380.9998035430908         49.99995231628418

In the above code, we have defined two lists and two numpy arrays. Then, we have compared the time taken in order to find the sum of lists and sum of numpy arrays both. If you see the output of the above program, there is a significant change in the two values. List took 380ms whereas the numpy array took almost 49ms. Hence, numpy array is faster than list. Now, if you noticed we had run a ‘for’ loop for a list which returns the concatenation of both the lists whereas for numpy arrays, we have just added the two array by simply printing A1+A2. That’s why working with numpy is much easier and convenient when compared to the lists.

Therefore, the above examples prove the point as to why you should go for python numpy array rather than a list!

Moving forward in python numpy tutorial, let’s focus on some of its operations.

Методы сортировки в Numpy

Мы узнаем приведенные ниже методы сортировки в Numpy.

1. Функция numpy sort ()
2. Функция numpy argsort ()
3. Функция numpy lexsort ()

Итак, давайте начнем!

1. функция numpy sort ()

Чтобы сортировать различные элементы, присутствующие в структуре массива, NUMPY предоставляет нам Сортировать () функция. С помощью функции Sort () мы можем отсортировать элементы и отделить их в порядке возрастания в порядок убывания соответственно.

Посмотрите на синтаксис ниже!

Синтаксис:

numpy.sort(array, axis)

Ось параметра «Оси» указывает способ выполнения сортировки. Поэтому, когда мы устанавливаем, сортировка происходит в традиционной моде, а результирующий массив является одним ряд элементов. С другой стороны, если мы установим, сортировка происходит в ряду моды, то есть каждая, и каждая строка сортируется индивидуально.

Пример 1:

В этом примере мы создали массив, далее мы отсортировали массив, используя Сортировка () Функция и с Ось I.e. Это сортирует элементы в порядке возрастания.

import numpy as np
data = np.array(, ])
res = np.sort(data, axis = None)        
print ("Data before sorting:", data)
print("Data after sorting:", res)

Выход:

Data before sorting: 
 ]
Data after sorting: 

Пример 2:

В этом примере мы создали массив и отсортировали то же самое, используя функцию сортировки (), здесь мы установили i.e. ROW WISE сортировка была выполнена.

import numpy as np
data = np.array(, ])
res = np.sort(data, axis = 1)        
print ("Data before sorting:", data)
print("Row wise sorting:", res)

Выход:

Data before sorting: 
 ]
Row wise sorting: 
 ]

2. Numpy argsort ()

Помимо метода Worth (), у нас также есть argsort () Функция, которая используется в качестве методов сортировки в Numpy, которая возвращает Массив индексов отсортированных элементов. Из этих сортировков значений индекса мы можем получить элементы отсортированного массива в порядке возрастания.

Таким образом, с функцией argsort () мы можем отсортировать значения массива и получать значения индекса того же, что и отдельный массив.

Пример:

import numpy as np
data = np.array()
res_index = np.argsort(data)        
print ("Data before sorting:", data)
print("Sorted index values of the array:", res_index)

x = np.zeros(len(res_index), dtype = int)
for i in range(0, len(x)):
    x= data]
print('Sorted array from indexes:', x)

Выход:

В приведенном выше примере мы выполнили функцию Argsort () на значениях данных и получили сортировку значений индекса элементов. Кроме того, мы использовали одинаковые значения индекса массива, чтобы получить элементы отсортированного массива.

Data before sorting: 
Sorted index values of the array: 
Sorted array from indexes: 

3. numpy lexsort () Функция

Функция Lexsort () позволяет отсортировать значения данных с использованием последовательности клавиш I.E. Столкомыми. С Lexsort () Функция, мы сортируем два массива, принимая по одному во время. В результате мы получаем индексные значения отсортированных элементов.

import numpy as np
data = np.array()
data1 = np.array()
res_index = np.lexsort((data1, data))        
print("Sorted index values of the array:", res_index)

Выход:

Sorted index values of the array: 

Синтаксис

Формат:

array = numpy.arange(start, stop, step, dtype=None)

Где:

• start -> Начальная точка (включенная) диапазона, которая по умолчанию установлена на 0;
• stop -> Конечная точка (исключенная) диапазона;
• step -> Размер шага последовательности, который по умолчанию равен 1. Это может быть любое действительное число, кроме нуля;
• dtype -> Тип выходного массива. Если dtype не указан (или указан, как None), тип данных будет выведен из типа других входных аргументов.

Давайте рассмотрим простой пример, чтобы понять это:

import numpy as np
 
a = np.arange(0.02, 2, 0.1, None)
 
print('Linear Sequence from 0.02 to 2:', a)
print('Length:', len(a))

Это сгенерирует линейную последовательность от 0,2 (включительно) до 2 (исключено) с размером шага 0,1, поэтому в последовательности будет (2 — 0,2) / 0,1 — 1 = 20 элементов, что является длиной результирующего массив numpy.

Вывод:

Linear Sequence from 0.02 to 2: 
Length: 20

Вот еще одна строка кода, которая генерирует числа от 0 до 9 с помощью arange(), используя размер шага по умолчанию 1:

>>> np.arange(0, 10)
array()

Если размер шага равен 0, это недопустимая последовательность, поскольку шаг 0 означает, что вы делите диапазон на 0, что вызовет исключение ZeroDivisionError Exception.

import numpy as np

# Invalid Step Size!
a = np.arange(0, 10, 0)

Вывод:

ZeroDivisionError: division by zero

ПРИМЕЧАНИЕ. Эта функция немного отличается от numpy.linspace(), которая по умолчанию включает как начальную, так и конечную точки для вычисления последовательности. Он также не принимает в качестве аргумента размер шага, а принимает только количество элементов в последовательности.

Тест производительности

Мы не должны чередовать векторизованную операцию numpy вместе с циклом. Это резко снижает производительность, так как код повторяется с использованием собственного.

Например, в приведенном ниже фрагменте показано, как не следует использовать numpy.

for i in np.arange(100):
    pass

Рекомендуемый способ – напрямую использовать операцию numpy.

np.arange(100)

Давайте проверим разницу в производительности с помощью модуля timeit.

import timeit
import numpy as np

# For smaller arrays
print('Array size: 1000')

# Time the average among 10000 iterations
print('range():', timeit.timeit('for i in range(1000): pass', number=10000))
print('np.arange():', timeit.timeit('np.arange(1000)', number=10000, setup='import numpy as np'))

# For large arrays
print('Array size: 1000000')

# Time the average among 10 iterations
print('range():', timeit.timeit('for i in range(1000000): pass', number=10))
print('np.arange():', timeit.timeit('np.arange(1000000)', number=10, setup='import numpy as np'))

Вывод:

Array size: 1000
range(): 0.18827421900095942
np.arange(): 0.015803234000486555
Array size: 1000000
range(): 0.22560399899884942
np.arange(): 0.011916546000065864

Как видите, numpy.arange() особенно хорошо работает для больших последовательностей. Это почти в 20 раз (!!) быстрее обычного кода Python для размера всего 1000000, который будет лучше масштабироваться только для больших массивов.

Следовательно, numpy.arange() должен быть единодушным выбором среди программистов при работе с большими массивами. Для небольших массивов, когда разница в производительности не так велика, вы можете использовать любой из двух методов.

Строки и столбцы для массива Numpy

ПРИМЕР:

From numpy import asarray
data = , ]
# convert to a numpy array(data)

# step through rows
for row in range(data.shape):
	print(data)

#step through columns
for col in range(data.shape):
	print(data)

ВЫХОД:

ОБЪЯСНЕНИЕ:

В приведенном выше примере мы перечисляем данные каждой строки и столбца. Другими словами, мы достигаем этого, получая доступ к ним через их индекс. Данные дают значение в первой строке и первом столбце. Кроме того, data дает значения в первой строке и во всех столбцах, например, полную первую строку в нашей матрице. Аналогично, data обращается ко всем строкам первого столбца. Прежде всего, при печати строк массива ось Numpy устанавливается в 0, то есть data.shape. Аналогично, ось Numpy устанавливается в 1 при перечислении столбцов.

Обратитесь в массив списка в Python

Как мы уже обсуждали Списки и Массивы похожи в Python. Там, где основное различие между ними, в том, что массивы позволяют только элементы одного и того же типа данных, в то время как списки позволяют им быть разными.

Поскольку Python не поддерживает обычные массивы, мы можем использовать списки, чтобы изобразить то же самое и попытаться отменить их. Давайте посмотрим на разные методы, следующие, которые мы можем достичь этой задачи,

1. Использование списка нарезка, чтобы изменить массив в Python

Мы можем изменить массив списка, используя нарезка методы. Таким образом, мы фактически создаем новый список в обратном порядке как у оригинального. Давайте посмотрим, как:

#The original array
arr = 
print("Array is :",arr)

res = arr #reversing using list slicing
print("Resultant new reversed array:",res)

Выход :

Array is : 
Resultant new reversed array: 

2. Использование метода обратного ()

Python также предоставляет встроенный метод Это непосредственно меняет порядок элементов списка прямо на исходном месте.

Примечание : Таким образом, мы меняем порядок фактического списка. Следовательно, исходный порядок потерян.

#The original array
arr = 
print("Before reversal Array is :",arr)

arr.reverse() #reversing using reverse()
print("After reversing Array:",arr)

Выход :

Before reversal Array is : 
After reversing Array: 

3. Использование обратного () метода

У нас еще один метод, Что при прохождении со списком возвращает намерение имеющих только элементы списка в обратном порядке. Если мы используем Метод на этом намечном объекте мы получаем новый список, который содержит наш обратный массив.

#The original array
arr = 
print("Original Array is :",arr)
#reversing using reversed()
result=list(reversed(arr))
print("Resultant new reversed Array:",result)

Выход :

Original Array is : 
Resultant new reversed Array: 

Минутка восхищения или что такого в массивах NumPy

Но, все-таки,
что такого в массивах NumPy, что они повсеместно используются в
разных библиотеках? Давайте я приведу несколько примеров, и вы сами все
увидите.

Предположим, мы
определили одномерный массив с числами от 1 до 9:

a = np.array(1,2,3,4,5,6,7,8,9)

Мы уже знаем как
взять один отдельный элемент, но что будет, если прописать индексы для всех 9
элементов:

a 1,1,1,1,1,1,1,1,1 

На выходе увидим
одномерный массив из двоек:

array()

Или, так:

a 1,1,1,1,1 

тогда получим
аналогичный массив, но размерностью 5 элементов:

array()

Как видите,
индексирование здесь более гибкое, чем у обычных списков Python. Или, вот еще один характерный пример:

a True, True, False, False, False, False, True, True, True 

Результат будет
следующим:

array()

То есть,
остаются элементы со значениями True и отбрасываются со значениями False. Обо всем этом
мы еще будем подробно говорить.

Еще один пример.
Предположим, нам понадобилось представить одномерный массив a в виде матрицы
3х3. Нет ничего проще, меняем его размерность:

b = a.reshape(3, 3)

и получаем
заветный результат:

array(,

      
,

       ])

Далее, можем
обращаться к элементам матрицы b так:

b12

или так:

b1, 2

В обоих случаях
будет взят один и тот же элемент со значением 6.

Все это лишь
мимолетный взгляд на возможности пакета NumPy. Я здесь лишь
хотел показать, насколько сильно отличаются массивы array от списков
языка Python, и если вы
хотите овладеть этим инструментом, то эта серия занятий для вас.

Видео по теме

#1. Пакет numpy — установка и первое знакомство | NumPy уроки

#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки

#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки

#4. Свойства и представления массивов, создание их копий | NumPy уроки

#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки

#6. Объединение и разделение массивов | NumPy уроки

#7. Индексация, срезы, итерирование массивов | NumPy уроки

#8. Базовые математические операции над массивами | NumPy уроки

#9. Булевы операции и функции, значения inf и nan | NumPy уроки

#10. Базовые математические функции | NumPy уроки

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки

#12. Множества (unique) и операции над ними | NumPy уроки

#13. Транслирование массивов | NumPy уроки

Ось Numpy для конкатенации двух массивов

Параметр axis, который мы используем с функцией numpy concatenate (), определяет ось, вдоль которой мы складываем массивы. Мы получаем различные типы сцепленных массивов в зависимости от того, установлено ли значение параметра оси равным 0 или 1. Кроме того, чтобы иметь более четкое представление о том, что говорится, обратитесь к приведенным ниже примерам.

Конкатенация Np массивов с осью 0

import numpy as np

#arrays defined.array(,]).array(,])

print(np_array_1)
print(np_array_2)
.concatenate(,)

print(a)

Выход:

array(,
       ])

array(,
       ])

array(,
       ,
       ,
       ])

Объяснение:

Как уже упоминалось, параметр axis в функции ‘concatenate()’ подразумевает укладку массивов. Поэтому, когда мы устанавливаем ось в 0, функция concatenate складывает два массива вдоль строк. Мы указываем, что хотим конкатенации массивов. Конкатенация выполняется вдоль оси 0, то есть вдоль направления строк. Таким образом, мы получаем результат в виде сложенного массива. И два составных массива вдоль рядов.

Конкатенация массивов Numpy с осью 1

import numpy as np

#arrays defined.array(,]).array(,])

print(np_array_1)
print(np_array_2)
.concatenate(,)

print(a)

Выход:

array(,
       ])

array(,
       ])

array(,
       ])

Объяснение:

В приведенном выше примере параметр axis имеет значение 1. Например, мы знаем, что ось 1 определяет направление вместе со столбцами. Прежде всего это подразумевает функцию numpy concatenate() для объединения двух входных данных href=”https://en.wikipedia.org/wiki/Array_data_structure”>массивы. После этого конкатенация выполняется горизонтально вместе со столбцами. href=”https://en.wikipedia.org/wiki/Array_data_structure”>массивы. После этого конкатенация выполняется горизонтально вместе со столбцами.

Примеры работы с NumPy

Подытожим все вышесказанное. Вот несколько примеров полезных инструментов NumPy, которые могут значительно облегчить процесс написания кода.

Математические формулы NumPy

Необходимость внедрения математических формул, которые будут работать с матрицами и векторами, является главной причиной использования NumPy. Именно поэтому NumPy пользуется большой популярностью среди представителей науки. В качестве примера рассмотрим формулу , которая является центральной для контролируемых моделей машинного обучения, что решают проблемы регрессии:

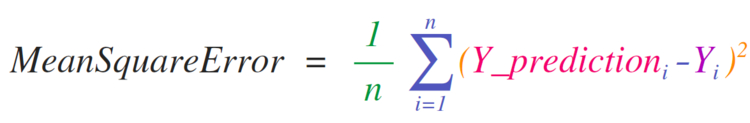
Реализовать данную формулу в NumPy довольно легко:

Главное достоинство NumPy в том, что его не заботит, если и содержат одно или тысячи значение (до тех пор, пока они оба одного размера). Рассмотрим пример, последовательно изучив четыре операции в следующей строке кода:

У обоих векторов и по три значения. Это значит, что в данном случае равно трем. После выполнения указанного выше вычитания мы получим значения, которые будут выглядеть следующим образом:

Затем мы можем возвести значения вектора в квадрат:

Теперь мы вычисляем эти значения:

Таким образом мы получаем значение ошибки некого прогноза и за качество модели.

Представление данных NumPy

Задумайтесь о всех тех типах данных, которыми вам понадобится оперировать, создавая различные модели работы (электронные таблицы, изображения, аудио и так далее). Очень многие типы могут быть представлены как n-мерные массивы:

Аргумент ключевого слова axis

Это устанавливает axis для сохранения образцов. Он используется только в том случае, если начальная и конечная точки относятся к типу данных массива.

По умолчанию (axis = 0) образцы будут располагаться вдоль новой оси, вставленной в начало. Мы можем использовать axis = -1, чтобы получить ось в конце.

import numpy as np

p = np.array(, ])
q = np.array(, ])

r = np.linspace(p, q, 3, axis=0)
print(r)
s = np.linspace(p, q, 3, axis=1)
print(s)

Вывод

array(,
        ],

       ,
        ],

       ,
        ]])

array(,
        ,
        ],

       ,
        ,
        ]])

В первом случае, поскольку axis = 0, мы берем пределы последовательности от первой оси.

Здесь пределы – это пары подмассивов и , а также и , берущие элементы из первой оси p и q. Теперь мы сравниваем соответствующие элементы из полученной пары, чтобы сгенерировать последовательности.

Таким образом, последовательности , ] для первой строки и ], ] для второй пары (строки), которая оценивается и объединяется для формирования , ], , ], , ]],

Во втором случае будут вставлены новые элементы в axis = 1 или столбцы. Таким образом, новая ось будет создана через последовательности столбцов. вместо последовательностей строк.

Последовательности с по и по рассматриваются и вставляются в столбцы результата, в результате чего получается , , ], , , ]].

Будучи генератором линейной последовательности, функция numpy.arange() в Python используется для генерации последовательности чисел в линейном пространстве с равномерным размером шага.

Это похоже на другую функцию, numpy.linspace() в Python, которая также генерирует линейную последовательность с одинаковым размером шага.

Давайте разберемся, как мы можем использовать эту функцию для генерации различных последовательностей.

Линейная алгебра

SciPy обладает очень быстрыми возможностями линейной алгебры, поскольку он построен с использованием библиотек ATLAS LAPACK и BLAS. Библиотеки доступны даже для использования, если вам нужна более высокая скорость, но в этом случае вам придется копнуть глубже.

Все процедуры линейной алгебры в SciPy принимают объект, который можно преобразовать в двумерный массив, и на выходе получается один и тот же тип.

Давайте посмотрим на процедуру линейной алгебры на примере. Мы попытаемся решить систему линейной алгебры, что легко сделать с помощью команды scipy linalg.solve.

Этот метод ожидает входную матрицу и вектор правой части:

# Import required modules/ libraries
import numpy as np
from scipy import linalg

# We are trying to solve a linear algebra system which can be given as:
#               1x + 2y =5
#               3x + 4y =6

# Create input array
A= np.array(,])

# Solution Array
B= np.array(,])

# Solve the linear algebra
X= linalg.solve(A,B)

# Print results
print(X)

# Checking Results
print("\n Checking results, following vector should be all zeros")
print(A.dot(X)-B)

Аудио и временные ряды в NumPy

По сути аудио файл  — это одномерный массив семплов. Каждый семпл представляет собой число, которое является крошечным фрагментов аудио сигнала. Аудио CD-качества может содержать 44 100 семплов в секунду, каждый из которых является целым числом в промежутке между -32767 и 32768. Это значит, что десятисекундный WAVE-файл CD-качества можно поместить в массив NumPy длиной в 10 * 44 100 = 441 000 семплов.

Хотите извлечь первую секунду аудио? Просто загрузите файл в массив NumPy под названием , после чего получите .

Фрагмент аудио файла выглядит следующим образом:

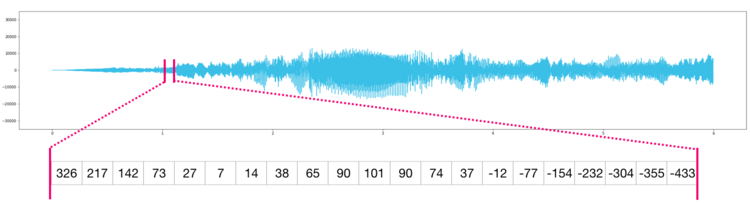
То же самое касается данных временных рядов, например, изменения стоимости акций со временем.

1.4.1.7. Fancy indexing¶

Tip

NumPy arrays can be indexed with slices, but also with boolean or
integer arrays (masks). This method is called fancy indexing.
It creates copies not views.

Using boolean masks

>>> np.random.seed(3)
>>> a = np.random.randint(, 21, 15)
>>> a
array()
>>> (a % 3 == )
array()
>>> mask = (a % 3 == )
>>> extract_from_a = amask # or,  a
>>> extract_from_a           # extract a sub-array with the mask
array()

Indexing with a mask can be very useful to assign a new value to a sub-array:

>>> aa % 3 ==  = -1
>>> a
array()

Indexing with an array of integers

>>> a = np.arange(, 100, 10)
>>> a
array()

Indexing can be done with an array of integers, where the same index is repeated
several time:

>>> a]  # note:  is a Python list
array()

New values can be assigned with this kind of indexing:

>>> a] = -100
>>> a
array()

Tip

When a new array is created by indexing with an array of integers, the
new array has the same shape as the array of integers:

>>> a = np.arange(10)
>>> idx = np.array(, 9, 7]])
>>> idx.shape
(2, 2)
>>> aidx
array(,
       ])

The image below illustrates various fancy indexing applications

Exercise: Fancy indexing

• Again, reproduce the fancy indexing shown in the diagram above.
• Use fancy indexing on the left and array creation on the right to assign
  values into an array, for instance by setting parts of the array in
  the diagram above to zero.

Операции со срезами matrix в Python

Часто мы работаем не с целым массивом, а с его компонентами. Эти операции выполняются с помощью метода слайс (срез). Он пришел на замену циклу for, при котором каждый элемент подвергался перебору. Метод позволяет получать копии matrix, причём манипуляции выполняются в виде . В данном случае start — индекс элемента, с которого берётся отсчёт, stop — последний элемент, step — размер шага или число пропускаемых значений элемента при каждой итерации. Изначально start равен нулю, stop — индексу последнего элемента, step — единице. Если выполнить операции без аргументов, копирование и добавление списка произойдёт полностью.

Допустим, имеем целочисленный массив otus = . Для копирования и вывода используем otus. В итоге произойдёт вывод последовательности . Но если аргументом станет отрицательное значение, допустим, -2, произойдёт вывод уже других данных:

otus-2]; //4 

Возможны и другие операции. Например, если добавить ещё одно двоеточие, будет указан шаг копируемых элементов. Таким образом, otus позволит вывести матрицу .

Если ввести отрицательное значение, к примеру, отсчёт начнётся с конца, и в результате произойдёт вывод . Остаётся добавить, что метод среза позволяет гибко работать с матрицами и вложенными списками в Python.

Хотите узнать гораздо больше? Записывайтесь на курс «Разработчик Python»!

Агрегирование в NumPy

Дополнительным преимуществом NumPy является наличие в нем функций агрегирования:

Функциями , и дело не ограничивается.

К примеру:

• позволяет получить среднее арифметическое;
• выдает результат умножения всех элементов;
• нужно для среднеквадратического отклонения.

Это лишь небольшая часть довольно обширного списка функций агрегирования в NumPy.

Использование нескольких размерностей NumPy

Все перечисленные выше примеры касаются векторов одной размерности. Главным преимуществом NumPy является его способность использовать отмеченные операции с любым количеством размерностей.