Деление в python

Что такое структура данных в языке программирования Python

Структуры данных в Python служат для написания программ, которые могут быть как простыми, так и достаточно сложными. Они бывают линейные, нелинейные и специфические.

К линейным структурам данных Python можно отнести массивы, матрицы, стек, очередь, связанный список. К нелинейным график, двоичное дерево, кучу, хэш-таблицу. Специфическими являются кортежи, словари, списки.

Также структуры данных в Питоне классифицируются как базовые, встроенные, динамические, упорядоченные, простейшие, собственные, общие, связанные.

Основные типы данных в Python это числа целые, с плавающей точкой, комплексные, строки, булев тип, тип none, исключения, байты, файлы, множества, функции, кортежи, словари, списки, строки.

Функция экспоненты exp() в Python

Библиотека Math в Python поставляется с функцией , которую можно использовать для вычисления значения . К примеру, — экспонента от . Значение равно .

Метод может быть использован со следующим синтаксисом:

Python

math.exp(x)

1	math.exp(x)

Параметр может быть положительным или отрицательным числом. Если не число, метод возвращает ошибку. Рассмотрим пример использования данного метода:

Python

import math

# Инициализация значений
an_int = 6
a_neg_int = -8
a_float = 2.00

# Передача значений методу exp() и вывод
print(math.exp(an_int))
print(math.exp(a_neg_int))
print(math.exp(a_float))

1 2 3 4 5 6 7 8 9 10 11

importmath   # Инициализация значений an_int=6 a_neg_int=-8 a_float=2.00   # Передача значений методу exp() и вывод print(math.exp(an_int)) print(math.exp(a_neg_int)) print(math.exp(a_float))

Вывод

Shell

403.4287934927351
0.00033546262790251185
7.38905609893065

1 2 3

403.4287934927351 0.00033546262790251185 7.38905609893065

Мы объявили три переменные и присвоили им значения с различными числовыми типами данных. Мы передали значения методу для вычисления их экспоненты.

Мы также можем применить данный метод для встроенных констант, что продемонстрировано ниже:

Python

import math

print(math.exp(math.e))
print(math.exp(math.pi))

1 2 3 4

importmath print(math.exp(math.e)) print(math.exp(math.pi))

Вывод

Shell

15.154262241479262
23.140692632779267

1 2	15.154262241479262 23.140692632779267

При передаче не числового значения методу будет сгенерирована , как показано далее:

Python

import math

print(math.exp(«20»))

1 2 3

importmath print(math.exp(«20»))

Вывод

Shell

Traceback (most recent call last):
File «C:/Users/admin/mathe.py», line 3, in <module>
print (math.exp(«20»))
TypeError: a float is required

1 2 3 4

Traceback(most recent call last) File»C:/Users/admin/mathe.py»,line3,in<module> print(math.exp(«20»)) TypeErrorafloatisrequired

Как видно из примера выше, генерируется ошибка .

2 ответа

Лучший ответ

Согласованность .

Вам нужно будет следовать некоторым очень простым и, казалось бы, неуместным объяснениям, чтобы понять это.

В школе вы выучили деление с остатком. И вы сделали расчеты следующим образом:

Позже вы выучили деления на действительные числа:

До этого момента вы можете полагать, что и всегда дают один и тот же результат. Это ваше текущее понимание ситуации.

Однако посмотрите, что происходит в целочисленном делении: число за R циклически изменяется от 3, 2, 1 до 0, а затем перезапускается: 3, 2, 1, 0. Число перед R уменьшается с каждым 4-м шагом.

Итак, как это будет продолжаться?

В то же время деление действительных чисел дает нам:

Вот почему дает -1, а дает 0.

Ну, они служат различным целям: является частью вычисления целых чисел с остатками, а дает вам часть перед операции с действительным числом.

Вы решаете, что вы хотите вычислить, затем вы решаете, какой оператор использовать в Python, чтобы получить правильный результат.

Хороший вопрос. Продолжайте учиться.

61

Thomas Weller
12 Дек 2019 в 12:56

Я бы сказал, что ваше наблюдение о том, что эти 2 операции должны быть интуитивно схожими, ожидается, поскольку при положительных числах они ведут себя одинаково. Но если вы посмотрите на их происхождение (одно из математики, а другое — из информатики), тогда будет более понятно их различное поведение.

Вы можете посмотреть там концепции:

• Этажное деление или функция пола, применяемое к математическому разделению
• Тип преобразования / Тип литья

================================================== ================

I) Этажное деление или функция пола, применяемая к математическому разделу

Функция пола — очень хорошо зарекомендовавшая себя концепция математики.

Из mathworld.wolfram:

Таким образом, разделение по этажам — это не более, чем функция по этажам, применяемая к математическому разделению. Поведение очень ясное, «математически точное».

II) Преобразование типов / приведение типов

Из википедии:

В большинстве языков программирования приведение формы с плавающей точкой к целому числу применяется правилом округления (поэтому существует соглашение):

Округление к 0 — направленное округление к нулю (также известное как усечение)

Правило округления в соответствии с IEEE 754.

Итак, другими словами, причина различия между целочисленным делением и преобразованием с плавающей точкой в int в python является математической, вот некоторые мысли от Гвидо ван Россума (думаю, мне не нужно его представлять: D) (из блог История Python, статья «Почему Python Целочисленное деление этажей «)

4

rusu_ro1
7 Янв 2020 в 22:09

Быстрый алгоритм Евклида

Но у этого
алгоритма есть один существенный недостаток: если мы введем два вот таких
числа:

100000000 и 2

то этот алгоритм
начнет довольно долго работать и понятно почему, здесь мы получим большое
количество вычитаний 2. Эти вычитания будут происходить до тех пор, пока двойка
укладывается в оставшееся число. И мы здесь без всяких вычитаний сразу можем
сказать, что на последнем шаге будет вот такая операция:

4-2 = 2

После чего оба
числа станут равными и НОД будет равен двум. Так вот, чтобы без лишних операций
сразу определить на сколько будут отличаться два числа после серии вычитаний,
достаточно взять целый остаток от деления. Например:

100000000 % 2 =
0

Это значит, что
большее число можно полностью составить из суммы двоек. Следовательно, они оба
делятся на два нацело и их НОД равен 2. Хорошо, а если вместо 2 взять 3. В этом
случае имеем:

100000000 % 3 =
1

и далее уже
можно рассматривать два числа: 3 и 1. Причем, для них также можно выполнить
такую же операцию:

3 % 1 = 1
1 % 1 = 0

Все, получили
НОД, равный 1. И смотрите, здесь на каждой итерации большее число делится на
меньшее. Поэтому быстрый алгоритм Евклида можно записать так:

пока меньшее число больше 0
        большему числу присваиваем остаток от деления на меньшее число
выводим большее число

Реализуем этот алгоритм. И договоримся, что большее число будем хранить в a, меньшее – в b.

a = int(input("Введите 1-е натуральное число: "))
b = int(input("Введите 2-е натуральное число: "))
sa = a; sb = b
b = min(sa, sb)
a = max(sa, sb)
while b:
    a,b = b, a%b
 
print("НОД(%d, %d) = %d"%(sa,sb,a))

В этом алгоритме
используется свойство:

a%b = c,  c < b

то есть, остаток
всегда будет меньше числа b. Значит, из двух чисел c и b большим будет b, а меньшим – c. Именно поэтому
в программе записано такое множественное присваивание:

a,b = b, a%b

Мы здесь переменной a
присваиваем
значение b, а b
становится
равным остатку от деления. Это гарантируется, что a
>=
b.

Видео по теме

Python 3 #1: установка и запуск интерпретатора языка

Python 3 #2: переменные, оператор присваивания, типы данных

Python 3 #3: функции input и print ввода/вывода

Python 3 #4: арифметические операторы: сложение, вычитание, умножение, деление, степень

Python 3 #5: условный оператор if, составные условия с and, or, not

Python 3 #6: операторы циклов while и for, операторы break и continue

Python 3 #7: строки — сравнения, срезы строк, базовые функции str, len, ord, in

Python 3 #8: методы строк — upper, split, join, find, strip, isalpha, isdigit и другие

Python 3 #9: списки list и функции len, min, max, sum, sorted

Python 3 #10: списки — срезы и методы: append, insert, pop, sort, index, count, reverse, clear

Python 3 #11: списки — инструмент list comprehensions, сортировка методом выбора

Python 3 #12: словарь, методы словарей: len, clear, get, setdefault, pop

Python 3 #13: кортежи (tuple) и операции с ними: len, del, count, index

Python 3 #14: функции (def) — объявление и вызов

Python 3 #15: делаем «Сапер», проектирование программ «сверху-вниз»

Python 3 #16: рекурсивные и лямбда-функции, функции с произвольным числом аргументов

Python 3 #17: алгоритм Евклида, принцип тестирования программ

Python 3 #18: области видимости переменных — global, nonlocal

Python 3 #19: множества (set) и операции над ними: вычитание, пересечение, объединение, сравнение

Python 3 #20: итераторы, выражения-генераторы, функции-генераторы, оператор yield

Python 3 #21: функции map, filter, zip

Python 3 #22: сортировка sort() и sorted(), сортировка по ключам

Python 3 #23: обработка исключений: try, except, finally, else

Python 3 #24: файлы — чтение и запись: open, read, write, seek, readline, dump, load, pickle

Python 3 #25: форматирование строк: метод format и F-строки

Python 3 #26: создание и импорт модулей — import, from, as, dir, reload

Python 3 #27: пакеты (package) — создание, импорт, установка (менеджер pip)

Python 3 #28: декораторы функций и замыкания

Python 3 #29: установка и порядок работы в PyCharm

Python 3 #30: функция enumerate, примеры использования

Создание десктопных приложений и UI

EEL

Для работы с созданием графических приложений есть несколько популярных библиотек, в частности встроенный tkinter и Qt. Но когда необходимо сделать красивое, легковесное графическое приложение, то хотелось бы использовать что-то более мощное, например, html+css+js, именно с этим может помочь библиотека EEL. Она позволяет создать десктопное приложение, где в качестве графической оболочки используется html, css и js (можно использовать различные фреймворки), а в качестве языка для написания бэк-части используется Python (подробнее тут).

Приведем простой пример использования библиотеки. Python код:

Файл index.html:

И сама структура проекта должна выглядеть так:

Можно запустить файл main.py и убедиться, что всё работает:

Логические операции с десятичным модулем

Decimal содержит набор встроенных функций для выполнения логических операций с десятичными числами, таких как AND, OR, XOR и т. Д.

• Функция logical_and(): выполняет операцию логического И над двумя десятичными числами и возвращает результат.
• Функция logical_or(): выполняет операцию логического ИЛИ над двумя десятичными числами и возвращает результат.
• Функция logical_xor(): выполняет логическую операцию XOR над двумя десятичными числами и возвращает результат.

#Syntax for logical_and() function-
decimal1.logical_and(decimal2)

#Syntax for logical_or() function-
decimal1.logical_or(decimal2)

#Syntax for logical_xor() function-
decimal1.logical_xor(decimal2)

Пример:

import decimal as d

valx = d.Decimal(1001)
valy = d.Decimal(1111)

print("Value 1: ",valx)
print("Value 2: ",valy)

AND = valx.logical_and(valy)
print("The logical AND value of the two decimals: ",AND)

OR = valx.logical_or(valy)
print("The logical OR value of the two decimals: ",OR)

XOR = valx.logical_xor(valy)
print("The logical XOR value of the two decimals: ",XOR)

Выход:

Value 1:  1001
Value 2:  1111
The logical AND value of the two decimals:  1001
The logical OR value of the two decimals:  1111
The logical XOR value of the two decimals:  110

Деление (/)

Сложение, вычитание и умножение тривиальны, а вот с делением не всё так просто. В Python существует три вида деления и столько же разных операторов. Начнём с истинного деления, за которое отвечает оператор «». Его главным отличием является то, что, вне зависимости от типов операндов, будет возвращен вещественный результат ().

Этот вид деления наиболее близок к обычному и знакомому нам математическому. И здесь тоже нельзя делить на ноль:

Немного истории. В старых версиях Питон оператор «/» выполнял операцию классического деления: т.е. он делил целочисленно и усекал дробную часть в том случае, когда делимое и делитель были целыми. Если же операнды принадлежали к множеству вещественных чисел, то проводилось деление с сохранением дробной части, и результат был float.

Разработчики отказались от классического деления в Python 3.0 и вместо него добавили истинное деление. Архитекторы языка пошли на такой шаг по той причине, что в предыдущей модели классического деления результаты напрямую зависели от типов операндов. Из-за этого возникали трудности с их предварительной идентификацией и оценкой, что было особенно критично для Питона, как для языка с динамической типизацией.

Реализация KNN в Python

Теперь, давайте попробуем реализовать концепцию KNN, чтобы решить проблему ниже регрессии.

Мы были предоставлены набором данных, который содержит исторические данные о количестве людей, которые решили арендовать велосипед в зависимости от различных условий окружающей среды.

Вы можете найти набор данных здесь .

Итак, давайте начнем!

1. Загрузите набор данных

Мы использовали использование Модуль пандас загрузить набор данных в среду, используя функция.

import pandas 
BIKE = pandas.read_csv("Bike.csv")

2. Выберите правильные функции

Мы использовали методику корреляции регрессионного анализа для выбора важных переменных из набора данных.

corr_matrix = BIKE.loc.corr()
print(corr_matrix)

Корреляционная матрица

               temp     atemp       hum  windspeed
temp       1.000000  0.991738  0.114191  -0.140169
atemp      0.991738  1.000000  0.126587  -0.166038
hum        0.114191  0.126587  1.000000  -0.204496
windspeed -0.140169 -0.166038 -0.204496   1.000000

Как «TEMP» и «ATEMP» очень коррелируют, мы бросаем «atemp» из набора данных.

BIKE = BIKE.drop(,axis=1)

3. Разделите набор данных

Мы использовали функцию reake_test_split () для разделения набора данных в 80% тренировках и набора данных на 20%.

#Separating the dependent and independent data variables into two data frames.
from sklearn.model_selection import train_test_split 

X = bike.drop(,axis=1) 
Y = bike

# Splitting the dataset into 80% training data and 20% testing data.
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.20, random_state=0)

4. Определите метрики ошибок

Поскольку это проблема регрессии, мы определили Maпе в виде метрик ошибок, как показано ниже-

import numpy as np
def MAPE(Y_actual,Y_Predicted):
    mape = np.mean(np.abs((Y_actual - Y_Predicted)/Y_actual))*100
    return Mape

5. Создайте модель

Содержит метод реализации KNN, как показано ниже-

#Building the KNN Model on our dataset
from sklearn.neighbors import KNeighborsRegressor
KNN_model = KNeighborsRegressor(n_neighbors=3).fit(X_train,Y_train)

Кроме того, мы предсказываем данные тестирования, используя функцию прогнозирования ().

KNN_predict = KNN_model.predict(X_test) #Predictions on Testing data

6. Проверка точности!

Мы называем описанную выше функцию Mape для проверки ошибки неправильной классификации и судить о точности прогнозов модели.

# Using MAPE error metrics to check for the error rate and accuracy level
KNN_MAPE = MAPE(Y_test,KNN_predict)
Accuracy_KNN = 100 - KNN_MAPE
print("MAPE: ",KNN_MAPE)
print('Accuracy of KNN model: {:0.2f}%.'.format(Accuracy_KNN))

Оценка точности KNN-

MAPE:  17.443668778014253
Accuracy of KNN model: 82.56%.

Сравнение двойной косой черты python с другими языками программирования

Каждый язык программирования решает целочисленное/целочисленное деление по-разному. Если мы попытаемся выполнить 5/2 в C++ или в Java, то получим следующий результат-

C++

#include 
using namespace std;
int main()
{
cout<<5/2;
return 0;
}

Выход-

2

Java-

public class Division{ 
  public static void main(String []args){
    System.out.println(5/2);
 }
}

Выход-

2

Как вы, должно быть, заметили, в отличие от python, здесь мы получаем 2.5 в качестве вывода. И если мы хотим получить наш результат в плавающих точках, нам нужно сделать href=”https://en.wikipedia.org/wiki/Divide”>разделите вот так – 5.0/2. href=”https://en.wikipedia.org/wiki/Divide”>разделите вот так – 5.0/2.

Преобразование в кортежи и списки

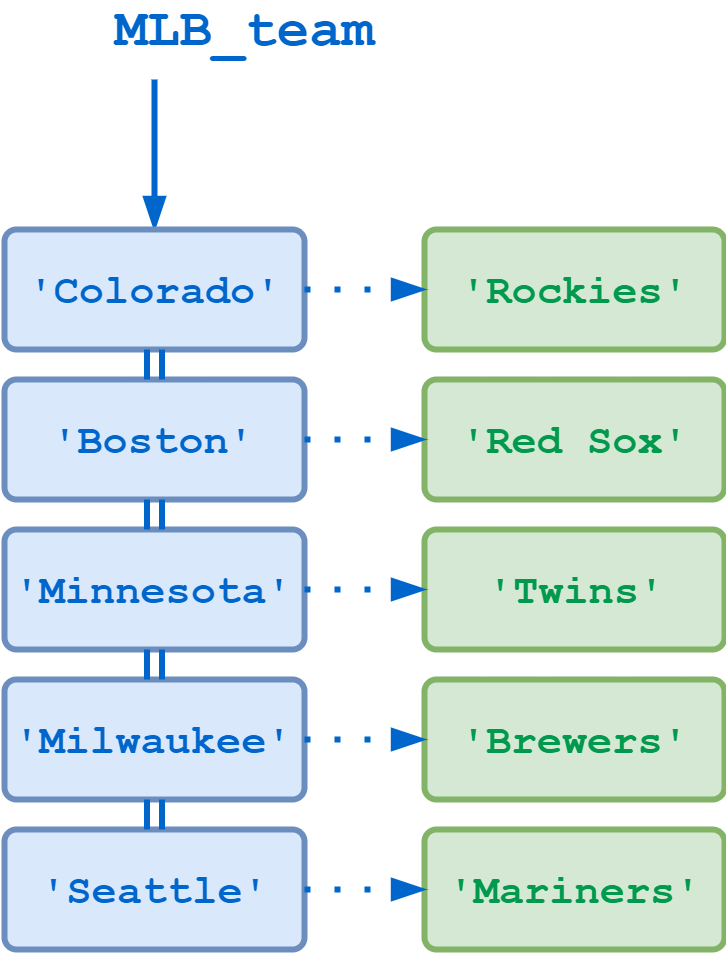
Вы можете использовать методы  и  для преобразования переданных им значений в тип данных списка и кортежа соответственно. В Python:

• список является изменяемой упорядоченной последовательностью элементов, заключенных в квадратные скобки .
• кортеж является неизменяемой упорядоченной последовательностью элементов, заключенных в круглые скобки .

Преобразование в кортежи

Начнем с преобразования списка в кортеж. Поскольку кортеж — это неизменяемый тип данных, такое преобразование может способствовать существенной оптимизации наших программ. Метод возвращает «кортежную» версию переданного ему значения.

print(tuple())

Мы видим, что в результате выводится кортеж, поскольку элементы теперь заключены в круглые, а не в квадратные скобки.

Давайте используем  с переменной, представляющей список:

sea_creatures = 
print(tuple(sea_creatures))

Опять же, мы видим, что значения списка преобразуются в значения кортежа, что обозначается круглыми скобками. 

Мы можем преобразовать в кортеж не только список, но и любой итерируемый тип, включая строки:

print(tuple('Sammy'))

Строки можно преобразовывать в кортежи с помощью метода , потому что они итерируемые (их можно перебирать). Но с типами данных, которые не являются итерируемыми (пример — целые числа и числа с плавающей запятой), мы получим ошибку:

print(tuple(5000))

Можно преобразовать целое число в строку, а затем в кортеж:  . Но лучше выбрать читаемый код, а не сложные преобразования.

Преобразование в списки

Преобразование значений, особенно кортежей, в списки может быть полезно, когда вам нужно иметь изменяемую версию этого значения. Для преобразования в список используется метод . 

Давайте преобразуем кортеж в список. Будьте внимательны со скобками: одна пара для кортежа, вторая — для метода  , а третья — для метода :

print(list(('blue coral', 'staghorn coral', 'pillar coral')))

Квадратные скобки сигнализируют о том, что кортеж, переданный в метод  , преобразован в список.

Чтобы сделать код более читабельным, мы можем ввести переменную и удалить одну из пар круглых скобок:

coral = ('blue coral', 'staghorn coral', 'pillar coral')
list(coral)

Если мы выведем , мы получим тот же результат, что и выше.

В список можно преобразовать не только кортеж, но и строку:

print(list('shark'))

Арифметические функции в Python

Арифметические функции используются для представления чисел в различных формах и осуществления над ними математических операций. Далее представлен перечень самых популярных арифметических функций:

• : округление определенного числа вверх;
• : возвращает модуль (абсолютное значение) указанного числа;
• : округление определенного числа вниз;
• : получение наибольшего общего делителя чисел и ;
• : возвращает сумму всех элементов итерируемого объекта;
• : возвращает (e^x)-1;
• : когда значение слишком мало, вычисление может привести к значительной потери в точности. может вернуть вывод с полной точностью.

В следующем примере показано использование перечисленных выше функций:

Python

import math

num = -4.28
a = 14
b = 8

num_list =
x = 1e-4 # Малое значение x

print(‘Число:’, num)
print(‘Округление числа вниз:’, math.floor(num))
print(‘Округление числа вверх:’, math.ceil(num))
print(‘Модуль числа:’, math.fabs(num))
print(‘Наибольший общий делитель a и b: ‘ + str(math.gcd(a, b)))
print(‘Сумма элементов списка: ‘ + str(math.fsum(num_list)))
print(‘e^x (при использовании функции exp()) равно:’, math.exp(x)-1)
print(‘e^x (при использовании функции expml()) равно:’, math.expm1(x))

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

importmath num=-4.28 a=14 b=8 num_list=10,8.25,75,7.04,-86.23,-6.43,8.4 x=1e-4# Малое значение x print(‘Число:’,num) print(‘Округление числа вниз:’,math.floor(num)) print(‘Округление числа вверх:’,math.ceil(num)) print(‘Модуль числа:’,math.fabs(num)) print(‘Наибольший общий делитель a и b: ‘+str(math.gcd(a,b))) print(‘Сумма элементов списка: ‘+str(math.fsum(num_list))) print(‘e^x (при использовании функции exp()) равно:’,math.exp(x)-1) print(‘e^x (при использовании функции expml()) равно:’,math.expm1(x))

Вывод

Python

Число: -4.28
Округление числа вниз: -5
Округление числа вверх: -4
Модуль числа: 4.28
Наибольший общий делитель a и b: 2
Сумма элементов списка: 16.029999999999998
e^x (при использовании функции exp()) равно: 0.0001000050001667141
e^x (при использовании функции expml()) равно: 0.00010000500016667084

1 2 3 4 5 6 7 8

Число-4.28 Округлениечиславниз-5 Округлениечиславверх-4 Модульчисла4.28 Наибольшийобщийделительaиb2 Суммаэлементовсписка16.029999999999998 e^x(прииспользованиифункцииexp())равно0.0001000050001667141 e^x(прииспользованиифункцииexpml())равно0.00010000500016667084

К числу других математических функций относятся:

• : принимает два вещественных аргумента, возводит первый аргумент в степень, значением которой является второй аргумент, после чего возвращает результат. К примеру, эквивалентно выражению ;
• : возвращает квадратный корень определенного числа.

Примеры данных методов представлены ниже:

Возведение в степень

Python

math.pow(3, 4)

1	math.pow(3,4)

Вывод

Shell

81.0

1

81.0

Квадратный корень

Python

math.sqrt(81)

1	math.sqrt(81)

Вывод

Shell

9.0

1

9.0

Выполнение операции деления

При делении результирующий вектор является значениями частного после выполнения операции деления над двумя векторами.

Для лучшего понимания рассмотрим приведенный ниже пример.

x = и y = – два вектора. Таким образом, результирующий вектор v будет таким:

v = x / y v = x / y .

Давайте теперь реализуем вышеуказанную концепцию.

Пример:

import numpy as np 
 
lst1 =  
lst2 = 
 
vctr1 = np.array(lst1) 
 
vctr2= np.array(lst2) 
 
print("Vector created from a list 1:") 
print(vctr1) 
print("Vector created from a list 2:") 
print(vctr2) 
 
vctr_div = vctr1/vctr2
print("Division of two vectors: ",vctr_div)

Вывод:

Vector created from a list 1:

Vector created from a list 2:

Multiplication of two vectors:  

Программа на Python, использующая библиотечные функции

Представим, мы стоим на расстоянии, например, 10 м, и наблюдаете за
тем как мяч поднимается в воздух после броска. Прямая соединяющая нас
и мяч составляет некий угол с горизонтальной прямой, величина которого
возрастает и убывает, когда мяч поднимается и опускается
соответственно. Давайте рассмотрим положение мяча в некоторый момент
времени, когда высота положения мяча равна 10 м.

Вычислим рассматриваемый нами угол. Перед тем как написать программу,
мы должны сформулировать некий алгоритм, т.е. некий способ
выполнения необходимых вычислений. В нашем случае, пусть \( x \) —
расстояние от нас до точки подброса мяча, а \( y \) — высота, на
которой находится мяч. Таким образом, образуется угол \( \theta \) с
поверхностью земли, где \( \mathrm{tg\,} \theta = y/x \). Следовательно,
\( \theta=\mathrm{arctg\,}(y/x) \).

Напишем сценарий выполняющий эти вычисления. Введем переменные и
для координат положения \( x \) и \( y \), и переменную
для угла \( \theta \). Сценарий сохраним в файл
ball_angle.py

# -*- coding: utf-8 -*-

x = 10   # горизонтальное положение
y = 10   # вертикальное положение

angle = atan(yx)

print (anglepi)*180

В этом сценарии строка иллюстрирует
вызов функции , соответствующей математической функции
\( \mathrm{arctg} \), с выражением в качестве аргумента
или входного параметра. Отметим, что тригонометрические функции
(такие как ) возвращают значение угла в радианах, поэтому для
преобразования результата в градусы мы использовали выражение
.

Теперь, запустив на выполнение сценарий, мы получим ошибку

NameError: name 'atan' is not defined

Очевидно, интерпретатор Python не распознал функцию , так как
эта функция еще не импортирована в программу. Достаточно большой
функционал доступен в интерпретаторе по умолчанию, однако намного
больший функционал реализован в библиотеках Python. Для того, чтобы
активировать использование дополнительного функционала, мы должны его
явно импортировать. В Python функция , как и множество других
математических функций, собраны в библиотеке . Такая
библиотека в терминах Python называется модулем. Чтобы мы могли
использовать функцию в нашем сценарии, мы должны написать

from math import atan

Добавив данную строку в начало сценария и запустив его, мы приходим к
другой проблеме: переменная не определена. Переменная ,
соответствующая значению \( \pi \), также определена в модуле , и
тоже должна быть импортирована

from math import atan, pi

Очевидно, что достаточно сложно импортировать поименно все необходимые
нам функции и переменные из модуля , поэтому существует
быстрый способ импортировать все из модуля :

from math import *

Мы будем использовать такое выражение для импорта, чтобы иметь доступ
ко всем общим математическим функциям. Таким образом рабочий сценарий
ball_angle.py имеет вид:

# -*- coding: utf-8 -*-
from math import *

x = 10   # горизонтальное положение
y = 10   # вертикальное положение

angle = atan(yx)

print (anglepi)*180

На первый взгляд кажется громоздким использование библиотек, так как
мы должны знать какой модуль импортировать, чтобы получить желаемый
функционал. Возможно, более удобно иметь доступ ко всему необходимому
в любое время. Однако это означает, что мы заполним память программы
большим количеством информации, которую мы будем редко использовать
для вычислений. Поэтому Python имеет большое количество библиотек,
реализующих огромные возможности, из которых мы можем импортировать
только необходимые в данный момент.

Что такое алгоритм KNN?

КНН – аббревиатура для к-ближайшего соседа. Это контролируемый алгоритм обучения машины. KNN в основном используется для классификации, а также регрессии.

KNN не предполагает какие-либо базовые параметры I.e. Это алгоритм.

Шаги, сопровождаемые алгоритмом KNN

• Изначально он хранит тренировочные данные в окружающую среду.
• Когда мы придумываем данные для прогнозирования, KNN выбирает K-самые одинаковые/аналогичные значения данных Для новой тестовой записи в соответствии с тренировочным набором данных.
• Кроме того, выбор K-самых подобных соседей для новой тестовой точки выполнен с использованием Отказ По сути, они рассчитывают расстояние между тестовой точкой и значениями данных тренировки, а затем выбирают k ближайших соседей.
• Наконец, значение тестового данных присваивается классу или группе, которая содержит максимальные точки K ближайших соседей тестовых данных.

Реальный пример K-NN

Заявление о проблеме – Рассмотрим сумку из бисера (тренировочные данные), имеющих два цвета – зеленый и синий.

Итак, здесь есть два класса: зеленый и синий. Наша задача – найти, к какому классу новое бусин «Z» упадет.

Решение – Первоначально мы случайным образом выбираем значение K. Давайте теперь предположим. Итак, KNN рассчитает расстояние Z со всеми значениями данных тренировки (сумка из бисера).

Кроме того, мы выбираем ближайшие значения 4 (k) к z, а затем попытайтесь проанализировать, к какому классу принадлежат большинство из 4 соседей.

Наконец, Z присваивается класс большинства соседей в пространстве.