Регрессионный анализ данных в excel

Задача о целесообразности покупки пакета акций

Множественная регрессия в Excel выполняется с использованием все того же инструмента «Анализ данных». Рассмотрим конкретную прикладную задачу.

Руководство компания «NNN» должно принять решение о целесообразности покупки 20 % пакета акций АО «MMM». Стоимость пакета (СП) составляет 70 млн американских долларов. Специалистами «NNN» собраны данные об аналогичных сделках. Было принято решение оценивать стоимость пакета акций по таким параметрам, выраженным в миллионах американских долларов, как:

• кредиторская задолженность (VK);
• объем годового оборота (VO);
• дебиторская задолженность (VD);
• стоимость основных фондов (СОФ).

Кроме того, используется параметр задолженность предприятия по зарплате (V3 П) в тысячах американских долларов.

Выполнение простой и множественной регрессии с помощью инструментов анализа данных Excel

В Excel очень легко выполнять линейную регрессию с помощью пакета инструментов Data Analytis.

Если вы у вас нет пакета инструментов (его можно увидеть на вкладке «Данные» в разделе «Анализ»), возможно, вам потребуется добавить инструмент.

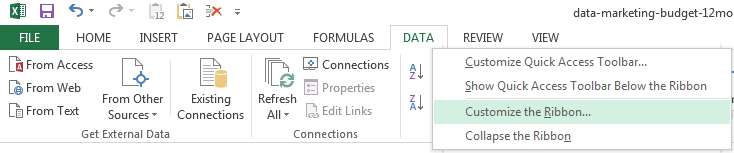
Перейдите на вкладку» Данные «, щелкните правой кнопкой мыши и выберите» Настроить ленту «.

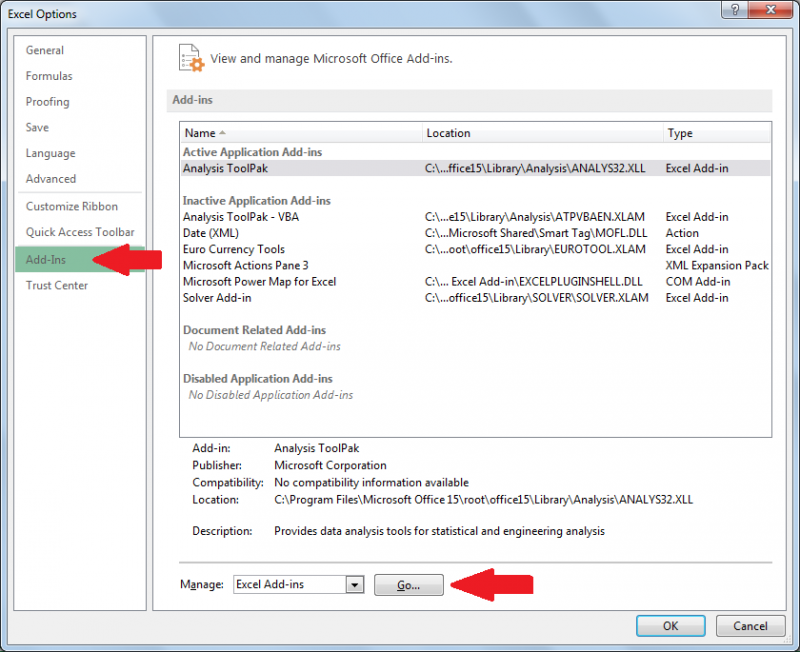
• Выберите надстройки и перейдите в раздел «Управление надстройками Excel».
• Затем выберите пакет инструментов анализа, и теперь он должен быть виден на вкладке «Данные».

Теперь, когда мы можем выбрать различные встроенные анализы, мы запустим инструмент регрессии.

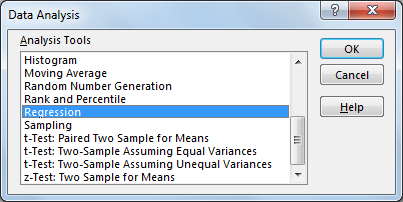
Если вы используете файл CSV или XSLX, вам следует отразить эти параметры.

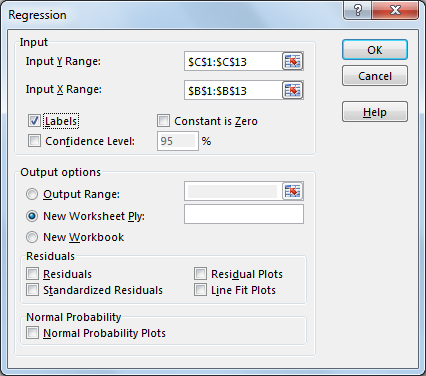
• Входной диапазон Y — это место, где находится переменная ответа (в нашем случае — продажи).
• Входной диапазон X равен диапазон переменных-предикторов (Spend).
• Проверяемые метки означают, что у вас есть заголовок в верхней части диапазона X и Y.

Дополнительные параметры, которые мы не проверили, это …

• Уровень достоверности — добавляет еще один доверительный интервал на выбранном уровне достоверности.
• Константа равно нулю — заставляет коэффициент X улавливать большую часть ошибки.
  • Практически нет причин использовать этот параметр, если только ваши данные не имеют теоретической причины проходить через источник.
  • Уравнение регрессии также фундаментально изменено (примечания к PDF)
• Остаточные значения — для каждой строки отображается ошибка/разница между прогнозируемыми и фактическими значениями. .
  • Стандартизированные остатки нормализованы со средним нулевым значением и стандартным отклонением, равным единице.
  • Графики остатков отображают остатки по каждой переменной.
  • График подгонки линии отображает прогнозируемые результаты и фактические результаты по каждой переменной.
• Графики нормальной вероятности — Проверяет n ормальность ваших данных. Должно быть видно что-то похожее на прямую.

После запуска инструмента регрессии Excel мы получим…

• Статистика регрессии — Статистика R-квадрат и стандартная ошибка.
• ANOVA — Проверка значимости модели.
• Переменные веса и статистика — дает вам веса коэффициентов, p-значение и доверительные границы для коэффициентов.

Теперь вы знаете, как выполнять линейную регрессию в Excel! Однако Excel — не лучший инструмент для интеллектуального анализа данных. Попробуйте R с открытым исходным кодом и выполните линейную регрессию в R.

Как интерпретировать результаты анализа

Ознакомиться с результатами регрессионного анализа можно в том месте, которое было указано в параметрах. Выглядит он таким приблизительно образом.

Самое главное значение, на которое мы будем ориентироваться – это R-квадрат. В нем записывается качество используемой модели. Чем он выше, тем оно выше. Если оно меньше 0,5, то зависимость считается плохой, если выше – то уже лучше. Чем ближе к 1, тем лучше. Соответственно, максимальный коэффициент – 1.

Также нужно обратить внимание на еще один важный показатель. Его можно найти в ячейке, которая находится на стыке строки Y-пересечение и колонки «Коэффициенты»

Здесь можно увидеть значение Y, которое будет равно нулю при определенных условиях. Также можно понять, насколько наша зависимая переменная является зависимой от факторов. Для этого нужно посмотреть, какая цифра стоит на пересечении граф Переменная X1» и «Коэффициенты». Чем коэффициент выше, тем лучше.

Видим, что программа Microsoft Excel открывает широкие возможности для регрессионного анализа. Но конечно, нужна дополнительная подготовка, чтобы читать эти результаты. Но если вы уже разбираетесь в статистике, то будет значительно проще. А теперь давайте приведем некоторые простые примеры, чтобы было более наглядно понятно, как линейная регрессия проводится на практике.

Основные задачи и виды регрессии

Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных. К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.

Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.

Основные задачи построения регрессионной модели заключаются в следующем:

1. Отбор значимых независимых переменных (Х1, Х2, …, Xk).
2. Выбор вида функции.
3. Построение оценок для коэффициентов.
4. Построение доверительных интервалов и функции регрессии.
5. Проверка значимости вычисленных оценок и построенного уравнения регрессии.

Регрессионный анализ бывает нескольких видов:

• парный (1 зависимая и 1 независимая переменные);
• множественный (несколько независимых переменных).

Уравнения регрессии бывает двух видов:

1. Линейные, иллюстрирующие строгую линейную связь между переменными.
2. Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.

Инструкция построения модели

Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:

Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ В MS EXCEL

1. Создайте файл исходных данных в MS Excel (например, таблица 2)

2. Построение корреляционного поля

Для построения корреляционного поля в командной строке выбираем меню Вставка/ Диаграмма . В появившемся диалоговом окне выберите тип диаграммы: Точечная ; вид: Точечная диаграмма , позволяющая сравнить пары значений (Рис. 22).

Рисунок 22 – Выбор типа диаграммы

Рисунок 23– Вид окна при выборе диапазона и рядов Рисунок 25 – Вид окна, шаг 4

2. В контекстном меню выбираем команду Добавить линию тренда.

3. В появившемся диалоговом окне выбираем тип графика (в нашем примере линейная) и параметры уравнения, как показано на рисунке 26.

Нажимаем ОК. Результат представлен на рисунке 27.

Рисунок 27 – Корреляционное поле зависимости производительности труда от фондовооруженности

Аналогично строим корреляционное поле зависимости производительности труда от коэффициента сменности оборудования. (рисунок 28).

от коэффициента сменности оборудования

3. Построение корреляционной матрицы.

Для построения корреляционной матрицы в меню Сервис выбираем Анализ данных.

С помощью инструмента анализа данных Регрессия , помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Для этого необходимо проверить доступ к пакету анализа. В главном меню последовательно выберите Сервис/ Надстройки . Установите флажок Пакет анализа (Рисунок 29)

Рисунок 30 – Диалоговое окно Анализ данных

После нажатия ОК в появившемся диалоговом окне указываем входной интервал (в нашем примере А2:D26), группирование (в нашем случае по столбцам) и параметры вывода, как показано на рисунке 31.

Результат расчетов представлен в таблице 4.

Разбор результатов анализа

Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.

Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.

Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.

Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.

Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:

ŷ — ожидаемое значение у при заданном значении х,

x — независимая переменная,

a — отрезок на оси y для прямой линии,

b — наклон прямой линии.

На рисунке ниже это понятие представлено графически:

На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.

Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением

На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4

Обратите внимание, что ожидаемое значение у в соответствии с линией при х
= 2 является ŷ. Мы можем подтвердить это с помощью следу­ющего уравнения:

ŷ = 2 + 0.5х =2 +0.5(2) =3.

Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.

Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по методу наименьших квадратов.

Простая математическая линейная регрессия вручную

В линейной регрессии всего несколько шагов .

1. Вычислить среднее значение переменной X.
2. Вычислить разницу между каждым X и средним X.
3. Возведите различия в квадрат и сложите все. Это SSxx.
4. Рассчитайте среднее значение вашей переменной Y.
5. Умножьте различия (X и Y на их соответствующие средние значения) и сложите их все вместе. Это SSxy.
6. Используя SSxx и SSxy, вы вычисляете перехват, вычитая SSxx/SSxy * AVG (X) из AVG (Y).

Используя пример набора данных, вот вычисления.

Месяц	Расходы	Avg (X) — X	(Avg (X) -X) ^ 2	Sales	Avg (Y) -Y	(Avg (X) -X) * (Avg (Y) -Y)
1	1000	5541.67	30,710,069,44	9914	60956.33	337 799 680,56
2	4000	2541,67	6,460,069,44	40487	30383,33	77 224 305,56
3	5000	1541,67	2 376 736,11	54324	16546,33	25 508 930,56
4	4500	2041,67	4 168 402,78	50044	20826,33	42 520 430,56
5	3000	3541,67	12 543 402,78	34719	36151.33	128 035 972,22
6	4000	2541,67	6,460,069,44	42551	28319,33	71,978,305,56
7	9000	— 2458,33	6 043 402,78	94871	-24000,67	59 001 638,89
8	11000	-4458,33	19 876 736,11	118914	-48043.67	214 194 680,56
9	15000	-8458.33	71 543 402,78	158484	-87613.67	741 065 597,22
10	12000	-5458,33	29 793 402,78	131348	-60477.67	330 107 263,89
11	7000	-458,33	210 069,44	78504	-7633,67	3 498 763,89
12	3000	3541.67	12 543 402. 78	36284	34586.33	122 493 263,89
AVG	6541. 67			70870.33
СУММ			202729166.67			2153428833.33

Поля суммы это наши SSxx и SSxy (соответственно). Чтобы вычислить коэффициент регрессии, мы разделим ковариацию X и Y (SSxy) на дисперсию X (SSxx)

Slope = SSxy/SSxx = 2153428833.33/202729166.67 = 10.62219546

Перехват — это «лишнее», которое модели необходимо компенсировать для среднего случая.

Intercept = AVG (Y) — Slope * AVG (X)

Intercept = 70870,33 — 10,62219546 * 6541,67 = 1,383,471380

Теперь у нас есть простое уравнение линейной регрессии.

Y = 1,383,471380 + 10,62219546 * X

Проверка общего качества уравнения множественной регрессии

Для этой цели, как и в случае множественной регрессии, используется коэффициентдетерминации R2:Справедливо соотношение 0 < =R2 < = 1. Чем ближе этот коэффициент к единице, тем больше уравнение множественной регрессии объясняет поведение Y.Для множественной регрессии коэффициент детерминации является неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение R2, так как каждая последующая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведениезависимой переменной.Иногда при расчете коэффициента детерминации для получения несмещенных оценок в числителе и знаменателе вычитаемой из единицы дроби делается поправка на число степеней свободы, т.е. вводится так называемый скорректированный (исправленный) коэффициент детерминации:Соотношение может быть представлено в следующем виде: для m>1. С ростом значения mскорректированный коэффициент детерминации растет медленнее, чем обычный.Очевидно, что только при R2 = 1. может принимать отрицательные значения. Доказано, что  увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t-статистика для этой переменной по модулю больше единицы. Поэтому добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.Рекомендуется после проверки общего качества уравнения регрессии провести анализ его статистической значимости. Для этого используется F-статистика:

Показатели F и R2 равны или не равен нулю одновременно. Если F=0, то R2=0, следовательно, величина Y линейно не зависит от X₁,X₂,…,X_m.Расчетное значение F сравнивается с критическим Fкр. Fкр, исходя из требуемого уровня значимости α и чисел степеней свободы v₁ = m и v₂ = n — m — 1, определяется на основе распределения Фишера. Если F > Fкр, то R2 статистически значим.

Использование возможностей табличного процессора «Эксель»

Анализу регрессии в Excel должно предшествовать применение к имеющимся табличным данным встроенных функций. Однако для этих целей лучше воспользоваться очень полезной надстройкой «Пакет анализа». Для его активации нужно:

• с вкладки «Файл» перейти в раздел «Параметры»;
• в открывшемся окне выбрать строку «Надстройки»;
• щелкнуть по кнопке «Перейти», расположенной внизу, справа от строки «Управление»;
• поставить галочку рядом с названием «Пакет анализа» и подтвердить свои действия, нажав «Ок».

Если все сделано правильно, в правой части вкладки «Данные», расположенном над рабочим листом «Эксель», появится нужная кнопка.

Основные задачи и виды регрессии

Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных.
К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.

Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.

Основные задачи построения регрессионной модели заключаются в следующем:

1. Отбор значимых независимых переменных (Х1, Х2, …, Xk).
2. Выбор вида функции.
3. Построение оценок для коэффициентов.
4. Построение доверительных интервалов и функции регрессии.
5. Проверка значимости вычисленных оценок и построенного уравнения регрессии.

Регрессионный анализ бывает нескольких видов:

• парный (1 зависимая и 1 независимая переменные);
• множественный (несколько независимых переменных).

Уравнения регрессии бывает двух видов:

1. Линейные, иллюстрирующие строгую линейную связь между переменными.
2. Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.

Инструкция построения модели

Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:

Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.

Пакет MS Excel
позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро

Важно понять, как интерпретировать полученные результаты.
Для построения модели регрессии необходимо выбрать пункт Сервис\Анализ данных\Регрессия (в Excel 2007
этот режим находится в блоке Данные/Анализ данных/Регрессия). Затем полученные результаты скопировать в блок для анализа.

Линия регрессии является графическим отражением взаимосвязи между явлениями. Очень наглядно можно построить линию регрессии в программе Excel.

Для этого необходимо:

1.Открыть программу Excel

2.Создать столбцы с данными. В нашем примере мы будем строить линию регрессии, или взаимосвязи, между агрессивностью и неуверенностью в себе у детей-первоклассников. В эксперименте участвовали 30 детей, данные представлены в таблице эксель:

1 столбик — № испытуемого

2 столбик — агрессивность
в баллах

3 столбик — неуверенность в себе
в баллах

3.Затем необходимо выделить оба столбика (без названия столбика), нажать вкладку вставка

,
выбрать точечная

, а из предложенных макетов выбрать самый первый точечная с маркерами

.

4.Итак у нас получилась заготовка для линии регрессии — так называемая — диаграмма рассеяния
. Для перехода к линии регрессии нужно щёлкнуть на получившийся рисунок, нажать вкладку конструктор,

найти на панели макеты диаграмм

и выбрать Ма
кет9

, на нем ещё написано f(x)

5.Итак, у нас получилась линия регрессии. На графике также указано её уравнение и квадрат коэффициента корреляции

6.Осталось добавить название графика, название осей. Также по желанию можно убрать легенду, уменьшить количество горизонтальных линий сетки (вкладка макет

, затем сетка

). Основные изменения и настройки производятся во вкладке Макет

Линия регрессии построена в MS Excel. Теперь её можно добавить в текст работы.

Регрессионный анализ — это статистический метод исследования, позволяющий показать зависимость того или иного параметра от одной либо нескольких независимых переменных. В докомпьютерную эру его применение было достаточно затруднительно, особенно если речь шла о больших объемах данных. Сегодня, узнав как построить регрессию в Excel, можно решать сложные статистические задачи буквально за пару минут. Ниже представлены конкретные примеры из области экономики.

Регрессионный анализ в Excel

Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

• линейной (у = а + bx);
• параболической (y = a + bx + cx 2 );
• экспоненциальной (y = a * exp(bx));
• степенной (y = a*x^b);
• гиперболической (y = b/x + a);
• логарифмической (y = b * 1n(x) + a);
• показательной (y = a * b^x).

Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты. R-квадрат – коэффициент детерминации

В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.

Линейная регрессия в программе Excel

Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.

Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y
означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x
– это различные факторы, влияющие на переменную. Параметры a
являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k
обозначает общее количество этих самых факторов.

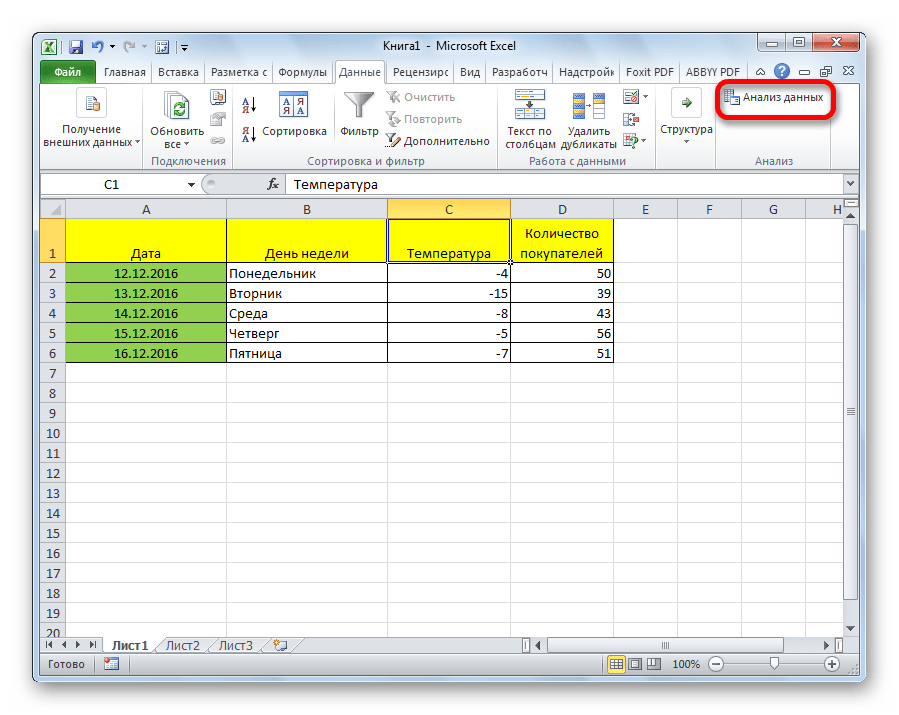
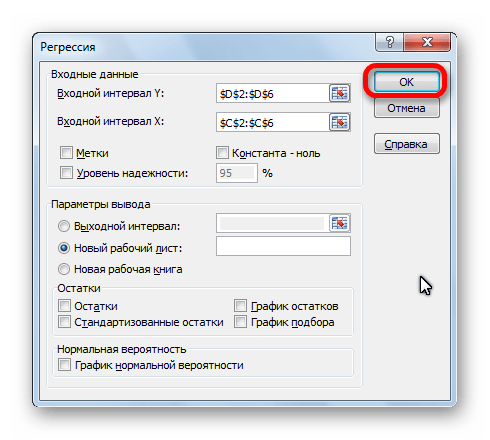
Линейная регрессия в Excel

Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:

• щелкаем по кнопке «Анализ данных»;
• в открывшемся окне нажимаем на кнопку «Регрессия»;
• в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
• подтверждаем свои действия нажатием кнопки «Ok».

В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии

Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных

Множественная линейная регрессия в MS Excel

В случае построения регрессионной зависимости некоторой случайной величины от совокупности нескольких случайных величин (одна зависимая переменная при нескольких независимых переменных) говорят о построении множественной линейной регрессии вида .

Рассмотрим следующую задачу.

Задача 3. Инвестиционная компания «Аргон-Инвест» рассматривает инвестиционный проект, связанный с покупкой 20%-ного пакета акций АО «N-ский металлургический комбинат». Стоимость пакета CП составляет 70 млн. USD. Менеджерами компании собрана информация об аналогичных сделках.

• Для оценки стоимости пакета акций ими выбраны следующие параметры:
• — стоимость основных фондов предприятия CОФ, млн. USD;
• — объем годового оборота предприятия VО, млн. USD;
• — кредиторская задолжненность предприятия VК, млн. USD;
• — дебиторская задолженность предприятия VД, млн. USD;

— задолженность предприятия по заработной плате VЗП, тыс. USD.

Для решения задачи 3 средствами MS Excel составляем таблицу исходных данных (рис. 10) и вызовем окно Анализ данных (рис. 1), где выбираем раздел Регрессия (рис. 11).

Параметры Входной интервал Y и Входной интервал X представляют собою зависимую и независимые переменные уравнения множественной линейной регрессии.

Результаты расчетов приведены на рис. 12.

1. По этим результатам может быть построено следующее уравнение регрессии
2. CP = 0,103CO + 0,541VO – 0,031VK +0,405VD +0,691VZP – 265,844
3. или
4. y = 0,103×1 + 0,541×2 – 0,031×3 +0,405×4 +0,691×5 – 265,844
5. Коэффициент множественной корреляции, коэффициент детерминации, критерий Фишера и критерий Стьюдента позволяют не отвергнуть гипотезу о линейном характере зависимости стоимости пакета акций предприятий от параметров приведенных в таблице.
6. Подставив соответствующие данные для N-ского металлургического комбината (таблица 1) в полученное уравнение регрессии получаем искомое значение стоимости пакета акций.
7. Таблица 1

СОФ, USD	VО, USD	VК, USD	VД, USD	VЗП, USD	CП, USD
102,50	535,50	45,20	41,50	21,55	64,72

Таким образом, стоимость пакета акций не должна превышать 64,72 млн. USD. То есть, инвестиционной компании «Аргон-Инвест» нецелесообразно приобретать предлагаемый пакет акций, так как его сумма завышена.

Не нашли то, что искали? Воспользуйтесь поиском: