6 лучших сервисов для построения графиков функций онлайн

Связанный график: повышение эффективности работы с Word

Способ будет полезен при необходимости часто менять исходные данные. Пошаговая инструкция:

1. Открыть таблицу Excel с нужными данными.

   Открываем таблицу Excel с нужными данными

2. Выделить необходимые ячейки, из которых будет построен график.

   Выделяем таблицу или отдельные ячейки для построения графика

3. Выбрать раздел «Вставка» и найти вкладку «Диаграмма».

   Выбираем раздел «Вставка», находим вкладку «Диаграмма»

4. Во вкладке «Диаграмма» найти значок «График», кликнуть по нему левым щелчком мышки.

   Находим значок «График», кликаем по нему левым щелчком мышки

5. Выделить созданный график. Достаточно щелкнуть по его границе.

   Выделяем созданный график, щелкнув мышкой по его границе

6. На вкладке «Главная» нажать «Буфер обмена».

   На вкладке «Главная» нажимаем «Буфер обмена»

7. Вырезать график.

   Левым кликом мышки нажимаем по значку ножниц

8. Вставить его в нужном месте текстового файла Word, щелкнув в «Буфере обмена» по иконке «Вставить», и выбрав подходящий параметр вставки.

   Во вкладке «Главная» в «Буфере обмена» кликаем по иконке «Вставить»

   Выбираем подходящий параметр вставки, при наведении на значки мышкой читаем название параметров

Подобный метод значительно упрощает работу с графическими данными. Буфер обмена позволяет сохранять нужные элементы и мгновенно перемещать их из одного текстового файла в другой. Помимо этого, создавать визуальные элементы в текстовом документе можно напрямую из табличного редактора Excel.

Видео — Как создать график Ворд, Эксель 2016

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Как решаем:

Упростим формулу функции:

Задача 2. Построим график функции

Как решаем:

Выделим в формуле функции целую часть:

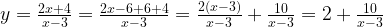
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Как решаем:

Вспомним, как параметры a, b и c определяют положение параболы.

1. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c = 0.

   Координата вершины

2. Ветви вверх, следовательно, a > 0.

   Точка пересечения с осью Oy — c = 0.

   Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

3. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c > 0.

   Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.

Задача 4. Построить графики функций:

а) y = 3x — 1

б) y = -x + 2

в) y = 2x

г) y = -1

Как решаем:

Воспользуемся методом построения линейных функций «по точкам».

а) y = 3x — 1

x	y
-1
1	2

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

б) y = -x + 2

x	y
2
1	1

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

в) y = 2x

x	y
1	2

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

г) y = -1

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Как решаем:

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

а) y = x² + 1

б)

в) y = (x — 1)² + 2

г)

д)

Как решаем:

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

y = x²

Сдвигаем график вверх на 1:

y = x² + 1

б)

Преобразование в одно действие типа f(x — a).

y = √x

Сдвигаем график вправо на 1:

y = √x — 1

в) y = (x — 1)² + 2

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

y = x²

Сдвигаем график вправо на 1:

y = (x — 1)²

Сдвигаем график вверх на 2:

y = (x — 1)² + 2

г)

Преобразование в одно действие типа

y = cos(x)

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

В детской школе Skysmart учиники чертят графики на специальной онлайн-доске. Учитель видит, как размышляет ученик и может вовремя его направить в нужную сторону.

Запишитесь на бесплатный вводный урок математики и занимайтесь в современном формате и с поддержкой заботливых учителей.

Нахождение возрастания и убывания, точек экстремума

Для решениянеравенства применяются промежутки возрастания и убывания с условиями f'(x)≥ и f'(x)≤ соответственно.

Определение 1

Стационарные точки – это такие точки, которые обращают производную в ноль.

Критические точки  — это внутренние точки из области определения, где производная функции равняется нулю или не существует.

При решении необходимо учитывать следующие замечания:

• при  имеющихся промежутках возрастания  и убывания неравенства вида  f'(x)> критические точки в решение не включаются;
• точки, в которых функция определена без конечной производной , необходимо включать в промежутки возрастания и убывания (к примеру, y=x3, где точка х= делает функцию определенной, производная имеет значение бесконечности в этой точке, y’=13·x23, y'()=1=∞, х= включается в промежуток возрастания);
• во избежание разногласий рекомендовано пользоваться математической литературой, которая рекомендована министерством образования.

Включение критических точек в промежутки возрастания и убывания в том случае, если они удовлетворяют области определения функции.

Определение 2

Для определения промежутков возрастания и убывания функции необходимо найти:

• производную;
• критические точки;
• разбить область определения при помощи критических точек на интервалы;
• определить знак производной на каждом из промежутков, где + является возрастанием, а — является убыванием.

Пример 3

Найти производную на области определения  f'(x)=x2′(4×2-1)-x24x2-1′(4×2-1)2=-2x(4×2-1)2.

Решение

Для решения нужно:

• найти стационарные точки, данный пример располагает х=;
• найти нули знаменателя, пример принимает значение ноль при x=±12.

Выставляем точки на числовой оси для определения производной   на каждом промежутке. Для этого достаточно взять любую точку из промежутка и произвести вычисление. При положительном результате на графике изображаем +, что означает возрастание функции, а — означает ее убывание.

Например, f'(-1)=-2·(-1)4-12-12=29>, значит, первый интервал слева имеет знак +. Рассмотрим на числовой прямой.

Ответ:

• происходит возрастание функции на промежутке -∞; -12 и (-12; ;
• происходит убывание на промежутке ; 12) и 12; +∞. 

На схеме при помощи + и — изображается положительность и отрицательность функции, а стрелочки – убывание и возрастание.

Точки  экстремума функции – точки, где функция определена и через которые производная меняет знак.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 4

Если рассмотреть пример, где х=, тогда значение функции в ней равняется f()=24·2-1=.  При перемене знака производной с + на — и прохождении через точку х=, тогда точка с координатами (; ) считается точкой максимума. При перемене знака с — на + получаем точку минимума.

Создаем диаграмму в диаграмме Excel

Приступим к выполнению каждого действия, производимого при построении комбинированных графиков, гистограмм или других типов диаграмм

Важно разобраться абсолютно с каждым шагом, ведь от этого зависит правильность отображения значений и удобство дальнейшей настройки

1. Вставка диаграммы производится уже после того, как все значения выделены, а значит, это нужно сделать прямо сейчас, зажав левую кнопку мыши и проведя курсором по всем блокам. Захватите и названия столбцов, чтобы они соответствовали названиям осей.

Когда все ячейки будут выделены, перейдите на вкладку «Вставка».

В разделе «Диаграммы» определитесь с тем, каким будет первый график.

Разверните весь список, посмотрите доступные варианты и нажмите по подходящему.

Диаграмма сразу же поместится в таблицу, а вы сможете заняться изменением ее размера и подбором подходящего расположения.

Разберемся с теми значениями, для которых и нужно создать график, отличающийся от первого. Изначально может сложиться такая ситуация, что из-за большой разницы в диапазоне значений его ось не будет видна в диаграмме, поэтому нужно ее настроить.

1. Кликните по ряду правой кнопкой мыши и в контекстном меню выберите пункт «Изменить тип диаграммы для ряда».

Отметьте галочкой пункт «Вспомогательная ось», которая и позволит нормализовать отображение.

Окно настройки можно не закрывать, поскольку оно еще пригодится, а вот изменения доступны для просмотра прямо вверху.

Теперь остается только изменить тип диаграммы, для чего разверните выпадающее меню «Тип диаграммы».

В таком же списке, как отображается на вкладке «Вкладка», найдите подходящую диаграмму и примените ее.

Вернитесь к таблице для проверки внесенных в диаграмму изменений.

Если же сводок значений больше двух, проделайте ту же операцию с другими рядами, предварительно подключив для них вспомогательные оси в случае проблем с правильностью отображения данных. Не бойтесь использовать совершенно разные виды диаграмм, чтобы каждый ряд выделялся и все сведения были понятны с первого взгляда.

Дополнительные настройки

В завершение пробежимся по основным настройкам, которые можно изменить в созданной комбинированной диаграмме. Например, вас не устраивает диапазон чисел, отображающийся по одной из осей. Для редактирования дважды нажмите по ней.

В появившемся окне ознакомьтесь с настройками вкладки «Параметры оси». Помимо визуальных изменений внизу есть и выбор разбежности в значениях, предоставляется возможность поработать с линиями или присутствующими столбцами.

Отдельный раздел называется «Параметры текста», где изменяется цвет надписей, общий стиль и другие опции. Посмотрите все настройки, которые здесь есть, чтобы подстроить внешнее отображение диаграмм под себя.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

ChartGo

Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.

Для обучения пользователям представляется подробное руководство и деморолики.

ChartGo будет полезен для тех, кто нуждается в создании диаграмм регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».

Построение графиков онлайн осуществляется по таблице.

В начале работы необходимо выбрать одну из разновидностей диаграмм.

Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.

Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.

Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.

Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.

Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.

Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков. При этом каждый график составлен с помощью точек и линий

Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.

Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.

Программа имеет гибко настраиваемый интерфейс.

После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.

7 Графики синуса и косинуса

Построим график функции . При этом нам опять пригодятся
часы из разд. 2.1.

Если , то, очевидно, . Когда возрастает от 0 до
, число возрастает от 0 до 1 (представьте себе,
как меняется ордината конца стрелки на наших фирменных часах).
Участок графика для от 0 до изображен на
рис. .
При

Чем ближе к , тем более полого идет наша кривая. Это
происходит потому, что проекция конца стрелки на ось
ординат, колеблясь по отрезку , быстрее всего
движется в середине отрезка и замедляется у его краев: мы
это уже обсуждали в разд. 2.1.

симметричны относительно прямой

Задача 7.1  
Запишите уравнение прямой, касающейся графика функции
в точке с координатами .

Кривая на рис б
центрально симметрична относительно точки
с координатами ; это следует из другой формулы
приведения:
(рис. б).

После того, как у нас есть участок графика функции для

, весь график строится уже просто. В самом деле,
когда конец стрелки прошел путь , стрелка вернулась
в исходное положение; при дальнейшем движении все будет
повторяться. Значит, график будет состоять из таких же кусков,
как на рис б. Окончательно график функции
выглядит так, как на рис. .

Теперь построим график функции . Можно было бы строить его так же, как
мы строили график синуса. Мы, однако, изберем другой путь,
который позволит использовать уже имеющуюся у нас информацию.

Именно, воспользуемся формулой приведения
. Эту формулу можно понимать так: функция
принимает те же значения, что и функция , но на
раньше. Например, функция принимает значение 1 при
, а функция
принимает это же
значение уже при . На графике это означает следующее: для
каждой точки графика есть точка графика ,
у которой ордината та же, а абсцисса на меньше
(рис. ).

сдвинуть график

Итак, мы выяснили, что график косинуса получается преобразованием
(сдвигом) из графика синуса. Случаи, когда график одной функции
можно получить преобразованием из графика другой функции,
интересны и сами по себе, поэтому скажем о них несколько слов.

Как, например, будет выглядеть график функции ? Ясно,
что ординаты точек этого графика получаются из ординат
соответствующих точек графика умножением на 2, так что
наш график изобразится сплошной кривой на рис. . Можно
сказать, что график получается из графика растяжением в два раза вдоль оси
ординат.

сжатием в 2 раза к оси ординат.

Попробуем еще построить график функции 
.
Понятно, что он должен получаться каким-то преобразованием из
графика . На первый взгляд может показаться, что это
преобразование — сдвиг влево на вдоль оси абсцисс, по
аналогии с тем, что изображено на рис. . Однако, если
бы это было так, то вышло бы, например, что функция

принимает значение 1 при

, что не соответствует действительности
(проверьте!). Правильно рассуждать так:
, так что функция
принимает те
же значения, что и функция , но на раньше. Так
что сдвиг влево — не на
, а на (рис. ).

Кривые, являющиеся графиками функций
, где ,
, называются синусоидами. Заметим, что кривой
«косинусоида» вводить не надо: как мы видели, график косинуса
— это та же кривая, что и график
синуса, только иначе
расположенная относительно осей координат.

Задача 7.2  
Каковы координаты точек, помеченных на
рис.  вопросительными знаками?

Задача 7.3  
Возьмите свечу, тонкий лист бумаги и острый нож. Намотайте лист
бумаги на свечу в несколько слоев и аккуратно разрежьте эту свечу
вместе с бумагой наискосок ножом. Теперь разверните бумагу. Вы
увидите, что она оказалась разрезанной по волнистой линии.
Докажите, что эта волнистая линия является синусоидой.

Задача 7.4  
Постройте графики функций:

Замечание. Если вы строите графики
тригонометрических функций на клетчатой бумаге, удобно выбрать
немного разные масштабы по осям, с тем чтобы на оси абсцисс
числу  соответствовало целое число клеточек. Например, часто
выбирают такой масштаб: по оси ординат отрезок длины 1 занимает
две клеточки, по оси абсцисс отрезок длины занимает 6
клеточек.

Задача 7.5  
Постройте графики функций:
а)
;
б)
.

Посмотрим, как выглядят на графиках уже известные нам решения
уравнений и . Эти решения являются
абсциссами точек пересечения горизонтальной прямой
с графиком функций (соответственно ). На
рис. , хорошо видны две серии решений,
получающихся при .

По графикам синуса и косинуса видно, на каких промежутках эти
функции возрастают, а на каких убывают. Ясно, например, что
функция возрастает на отрезках
,

,
,…- одним словом, на
всех отрезках
, где
,
и убывает на всех отрезках
, где

.

Задача 7.6  
На каких отрезках возрастает и на каких убывает
функция ?

Задача 7.7  
Сравните числа:

Задача 7.8  
Расположите в порядке возрастания:
, , , , , .

        Написать комментарий

Графики обратных тригонометрических функций

Построим график арксинуса

Перечислим основные свойства функции :

Область определения: , не существует значений вроде  или

Область значений: , то есть,  функция  ограничена.

Арксинус – функция нечетная, здесь минус опять же выносится: .

В практических вычислениях полезно помнить следующие значения арксинуса: , , . Другие распространенные значения арксинуса (а также других «арков») можно найти с помощью таблицы значений обратных тригонометрических функций.

Построим график арккосинуса

Очень похоже на арксинус, свойства функции сформулируйте самостоятельно. Остановлюсь на единственном моменте. В данной статье очень много разговоров шло о четности  и нечетности функций, и, возможно, у некоторых сложилось впечатление, что функция обязательно должна быть четной или нечетной. В общем случае, это, конечно, не так. Чаще всего, функция, которая вам встретится на практике – «никакая». В частности, арккосинус не является четной или нечетной функцией, он как раз «никакой».

Построим график арктангенса

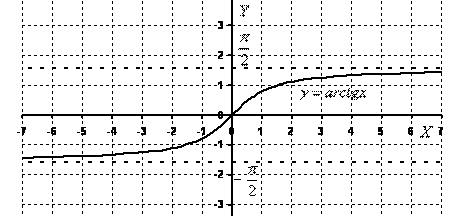
Всего лишь перевернутая ветка тангенса.
Перечислим основные свойства функции :

Область определения:

Область значений: , то есть,  функция  ограничена.
У рассматриваемой функции есть две асимптоты: , .

Арктангенс – функция нечетная: .

Самые «популярные» значения арктангенса, которые встречаются на практике, следующие: , .

К графику арккотангенса  приходится обращаться значительно реже, но, тем не менее, вот его чертеж:

Свойства арккотангенса вы вполне сможете сформулировать самостоятельно. Отмечу,  что арккотангенс, как и арккосинус, не является четной или нечетной функцией.

Пожалуй, для начала хватит. К этой странице придется частенько обращаться в ходе изучения самых различных разделов курса высшей математики.

Ну что, смертнички, полетаем? =)

Тогда надеваем парашюты и готовимся к преобразованиям графиков.

Желаю успехов!

(Переход на главную страницу)

Элементарный график изменения

График необходим, если от человека требуется продемонстрировать, насколько определенный показатель изменился за конкретный период времени. И обычного графика для выполнения этой задачи вполне достаточно, а вот различные вычурные диаграммы на деле могут только сделать информацию менее читаемой.

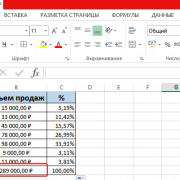
Предположим, у нас есть таблица, которая предоставляет информацию о чистой прибыли компании за последние пять лет.

Затем отправьтесь к вкладке «Вставка», где у вас есть возможность осуществить выбор типа графика, который будет подходящим в конкретной ситуации.

2

Нас интересует тип «График». После нажатия на соответствующую кнопку, появится окошко с настройками внешнего вида будущего графика. Чтобы понять, какой вариант подходит в конкретном случае, вы можете навести указатель мыши на определенный тип, и появится соответствующее приглашение.

После выбора нужного вида диаграммы вам необходимо скопировать таблицу данных связать ее с графиком. Результат будет следующим.

В нашем случае на диаграмме представлено две линии. Первая имеет красный цвет. Вторая – синий. Последняя нам не нужна, поэтому мы можем удалить ее, выбрав ее и нажав кнопку «Удалить». Поскольку мы имеем лишь одну линию, легенда (блок с названиями отдельных линий графика) также может быть удалена. Но маркеры лучше назвать. Найдите панель «Работа с диаграммами» и блок «Подписи данных» на вкладке «Макет». Здесь вы должны определить положение чисел.

Оси рекомендуется называть, чтобы обеспечить большую удобочитаемости графика. На вкладке «Макет» найдите меню «Названия осей» и задайте имя для вертикальной или горизонтальной осей соответственно.

Но вы можете смело обходиться без заголовка. Чтобы удалить его, вам нужно переместить его в область графика, которая невидима для постороннего глаза (над ним). Если вам все еще нужно название диаграммы, вы можете получить доступ ко всем необходимым настройкам через меню «Название диаграммы» на той же вкладке. Вы также можете найти его на вкладке «Макет».

Вместо порядкового номера отчетного года достаточно оставить только сам год. Выберите требуемые значения и щелкните по ним правой кнопкой мышки. Затем кликните по пункту «Выбор данных» – «Изменить подпись горизонтальной оси». Далее вам следует задать диапазон. В случае с нами, это первая колонка таблицы, являющейся источником информации. Результат такой.

Но вообще, можно все оставить, этот график вполне рабочий. Но если есть необходимость сделать привлекательный дизайн графика, то к вашим услугам – Вкладка “Конструктор”, которая позволяет указать фоновый цвет графика, его шрифт, а также разместить его на другом листе.

Полный пример решения онлайн

Лучшее спасибо — порекомендовать эту страницу

Провести полное исследование и построить график функции
$$
y(x)=\frac{x^2+8}{1-x}.
$$

1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, \quad \Rightarrow \quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-\infty; 1) \cup (1;+\infty).
$$

2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:

Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.

3) Определим точки пересечения графика функции с осями координат.

Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:

Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.

Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:

Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.

Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x \in (-\infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x \in (1; +\infty)$ функция $y\lt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).

4) Функция не является ни четной, ни нечетной, так как:

5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.

6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:

Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):

Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:

При $x \in (-\infty; -2), (4;+\infty)$ производная $y’ \lt 0$, поэтому функция убывает на данных промежутках.

При $x \in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.

При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).

Найдем значения функции в этих точках:

Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.

7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:

Приравняем вторую производную к нулю:

Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x \in (-\infty; 1)$ выполняется $y» \gt 0$, то есть функция вогнутая, когда $x \in (1;+\infty)$ выполняется $y» \lt 0$, то есть функция выпуклая.

8) Исследуем поведение функции на бесконечности, то есть при .

Так как пределы бесконечны, горизонтальных асимптот нет.

Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:

Получили, у что функции есть одна наклонная асимптота $y=-x-1$.

9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.

10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):

Нахождение промежутков выпуклости и вогнутости функции и точек перегиба

Выпуклость и вогнутость определяется при решении неравенств вида f»(x)≥ и f»(x)≤. Реже используют название выпуклость вниз вместо вогнутости, а выпуклость вверх вместо выпуклости.

Определение 3

Для определения промежутков вогнутости и выпуклости необходимо:

• найти вторую производную;
• найти нули функции второй производной;
• разбить область определения появившимися точками на интервалы;
• определить знак промежутка.

Пример 5

Найти вторую производную из области определения.

Решение

f»(x)=-2x(4×2-1)2’==(-2x)'(4×2-1)2—2x4x2-12′(4×2-1)4=24×2+2(4×2-1)3

Находим нули числителя и знаменателя, где на примере нашего примера имеем, что нули знаменателя x=±12

Теперь необходимо нанести точки на числовую ось и определить знак второй производной из каждого промежутка. Получим, что

Ответ:

• функция является выпуклой из промежутка -12; 12;
• функция является вогнутой из промежутков -∞; -12 и 12; +∞.

Определение 4

Точка перегиба – это точка вида x; f(x). Когда в ней имеется касательная к графику функции, то при ее прохождении через x функция изменяет знак на противоположный.

Иначе говоря, это такая точка, через которую проходит вторая производная  и меняет знак, а в самих точках равняется нулю или не существует. Все точки считаются областью определения функции.

В примере было видно, что точки перегиба отсутствуют, так как вторая производная изменяет знак во время прохождения через точки x=±12. Они , в свою очередь, в область определения не входят.

Создание графика с несколькими кривыми

Предположим, нам надо продемонстрировать инвесторам не одну лишь чистую прибыль предприятия, но и то, сколько в общей сумме будут стоить ее активы. Соответственно, выросло количество информации. 

9

Невзирая на это, в методике создания графика принципиальных отличий нет по сравнению с описанным выше. Просто теперь легенду надо оставить, поскольку ее функция отлично выполняется.

10

Создание второй оси

Какие же действия необходимо предпринять, чтобы создать еще одну ось на графике? Если мы используем общие метрические единицы, то необходимо применить советы, описанные ранее. Если применяются данные различных типов, то придется добавлять еще одну ось.

Но перед этим нужно построить обычный график, как будто используются одни и те же метрические единицы.

11

После этого главная ось выделяется. Затем вызовите контекстное меню. В нем будет много пунктов, один из которых – «Формат ряда данных». Его нужно нажать. Затем появится окно, в котором необходимо найти пункт меню «Параметры ряда», а далее выставить опцию «По вспомогательной оси».

12

Далее закройте окно. 

13

Но это всего лишь один из возможных методов. Никто не мешает, например, использовать для вторичной оси диаграмму другой разновидности. Надо определиться, какая линия требует того, чтобы мы добавили дополнительную ось, и потом кликнуть правой кнопкой мыши по ней и выбрать пункт «Изменить тип диаграммы для ряда».

14

Далее нужно настроить «внешность» второго ряда. Мы решили остановиться на линейчатой диаграмме.

15

Вот, как все просто. Достаточно сделать лишь пару кликов, и появляется еще одна ось, настроенная под иной параметр.