Кредитный калькулятор excel с досрочным погашением

Правила использования функции ОСПЛТ в Excel

Функция ОСПЛТ имеет следующий синтаксис:

=ОСПЛТ(ставка;период;кпер;пс;;)

Описание аргументов:

• ставка – обязательный для заполнения, принимает числовое значение процентной ставки в отношении финансового продукта (например, банковского кредита. Задается в виде десятичной дроби. Например, если кредит был взят по 17%, необходимо ввести значение 0,17;
• период – обязательный для заполнения, принимает числовые значения из диапазона от 1 до числа, указанного в качестве следующего аргумента рассматриваемой функции (кпер);
• кпер – обязательный для заполнения, принимает числовое значение, указывающее число периодов платежей в отношении финансового продукта;
• пс – обязательный для заполнения, принимает значение текущей стоимости финансового продукта, то есть суммы кредита, которую клиент должен вернуть банковской организации после заключения договора;
• – необязательный для заполнения, принимает значение будущей стоимости финансового продукта на момент совершения последнего платежа по утвержденной схеме платежей. Если явно не указан, принимается значение, равное 0 (нулю). Значение 0 означает, что задолженность будет выплачена в полном объеме;
• – необязательный для заполнения, принимает значения 0 или 1, указывающие на способ совершения платежей (в конце или начале периода). Если явно не указан, принимает значение 0.

Примечания:

1. Если аргумент период принимает значение не из диапазона , функция ОСПЛТ вернет код ошибки #ЧИСЛО!
2. Обязательные аргументы могут быть указаны в виде чисел, а также значений текстовых или других типов данных, которые могут быть преобразованы к числовым. Например, записи =ОСПЛТ(0,12;ИСТИНА;12;1000) или =ОСПЛТ(0,17;«4»;10;32000) являются допустимыми.
3. При указании аргументов ставка и кпер необходимо согласовывать единицы измерения этих показателей с учетом периодичности выплат. Например, для кредита, оформленного сроком на 1 год со ставкой 23% и ежемесячными платежами аргументы ставка и кпер функции ОСПЛТ должны быть заданы как 0,23/12 и 1*12 соответственно.

Объяснение финансовых функций, используемых в ипотечном калькуляторе

Функции PMT, IPMT и PPMT — по кредиту с постоянной процентной ставкой и оплатой

• ГУП рассчитывает общую сумму платежа.
• IPMT рассчитывает выплату процентов за заданный период.
• PPMT рассчитывает основной платеж за определенный период.

Синтаксис этих функций:

• = ПЛТ (ставка, количество платежей, приведенная стоимость, , )
• = IPMT (ставка, период, количество платежей, текущая стоимость, , )
• = PPMT (ставка, период, количество платежей, приведенная стоимость, , )

Где:

• Показатель: ежемесячная процентная ставка по кредиту.
• Период: период, за который вы хотите рассчитать проценты или основную сумму.
• Количество платежей: общее количество выплат по кредиту.
• Текущее значение: текущая стоимость будущих платежей.
• Будущая стоимость: будущая стоимость, которую вы хотите получить после последней оплаты. Если вы не укажете это значение, последнее значение будет нулевым.
• Тип: указывает срок платежа. (0 — конец периода, 1 — начало периода.)

Процесс создания ипотечного графика в Microsoft Excel относительно прост, хотя он использует некоторые сложные финансовые функции.

Начните с создания простого рабочего листа, в который будут вводиться данные и рассчитываться амортизация. В этом примере добавьте основные переменные, такие как сумма ссуды, количество месяцев, процентная ставка и т. Д., А также заголовки для фактического графика погашения. Сделать это:

Создайте диапазон с основными сведениями о ссуде: общая ссуда, процентная ставка, месяцы. Это переменные, которые позволят моделировать различные сроки кредита.
Добавьте к этому диапазону общий ежемесячный платеж, общий объем платежей и общий процент выплаченных процентов — они будут рассчитаны позже.
Создайте фактический график, добавив заголовок: «Месяц», «Начальный баланс», «Основная сумма», «Проценты», «Дополнительный платеж», «Конечный баланс» и «Общий платеж». После добавления формул в этом разделе будет автоматически рассчитан график погашения на основе переменных, введенных в основной диапазон ссуд.
Добавьте к диапазону сумму ссуды, процентную ставку и количество месяцев. Это делается для того, чтобы формулы работали и могли принимать любые значения.
Отформатируйте заголовки и диапазон.
Добавьте формулу = -PMT (C3 / 12, C4, C2) в ячейку C5 (см

Объяснение PMT справа) ВАЖНОЕ ПРИМЕЧАНИЕ: проценты в основном диапазоне — это годовые проценты. Разделите это значение на 12, чтобы получить ежемесячную процентную ставку, используемую в формуле)

Базовый формат завершен. Другие элементы, которые можно добавить (см. Выше снимок экрана для примера более сложного итогового рабочего листа):

• Оплата PMI
• Ежемесячный страховой платеж
• Налог на недвижимость

Дифференцированные платежи по кредиту в MS EXCEL. Примеры и методы

Составим в MS EXCEL график погашения кредита дифференцированными платежами.

При расчете графика погашения кредита дифференцированными платежами сумма основного долга делится на равные части пропорционально сроку кредитования. Регулярно, в течение всего срока погашения кредита, заемщик выплачивает банку эти части основного долга плюс начисленные на его остаток проценты. Если кредитным договором период погашения установлен равным месяцу, то из месяца в месяц сумма основного долга пропорционально уменьшается. Поэтому при дифференцированных платежах основные расходы заемщик несет в начале кредитования, размеры ежемесячных платежей в этот период самые большие. Но постепенно, с уменьшением остатка ссудной задолженности, уменьшается и сумма начисленных процентов по кредиту. Выплаты по кредиту значительно сокращаются и становятся не такими обременительными для заемщика.

Примечание. При расчете кредита дифференцированными платежами сумма переплаты по процентам будет ниже, чем при аннуитетных платежах. Не удивительно, что сегодня практически все российские банки применяют в расчетах аннуитетную схему погашения кредита. Сравнение двух графиков погашения кредита приведено в статье Сравнение графиков погашения кредита дифференцированными аннуитетными платежами в MS EXCEL.

График погашения кредита дифференцированными платежами

Задача. Сумма кредита =150т.р. Срок кредита =2 года, Ставка по кредиту = 12%. Погашение кредита ежемесячное, в конце каждого периода (месяца).

Решение. Сначала вычислим часть (долю) основной суммы кредита, которую заемщик выплачивает за период: =150т.р./2/12, т.е. 6250р. (сумму кредита мы разделили на общее количество периодов выплат =2года*12 (мес. в году)).Каждый период заемщик выплачивает банку эту часть основного долга плюс начисленные на его остаток проценты. Расчет начисленных процентов на остаток долга приведен в таблице ниже – это и есть график платежей.

Для расчета начисленных процентов может быть использована функция ПРОЦПЛАТ(ставка;период;кпер;пс), где Ставка — процентная ставка за период; Период – номер периода, для которого требуется найти величину начисленных процентов; Кпер — общее число периодов начислений; ПС – приведенная стоимость на текущий момент (для кредита ПС — это сумма кредита, для вклада ПС – начальная сумма вклада).

Примечание. Не смотря на то, что названия аргументов совпадают с названиями аргументов функций аннуитета – ПРОЦПЛАТ() не входит в группу этих функций (не может быть использована для расчета параметров аннуитета).

Примечание. Английский вариант функции — ISPMT(rate, per, nper, pv)

Функция ПРОЦПЛАТ() предполагает начисление процентов в начале каждого периода (хотя в справке MS EXCEL это не сказано). Но, функцию можно использовать для расчета процентов, начисляемых и в конце периода для это нужно записать ее в виде ПРОЦПЛАТ(ставка;период-1;кпер;пс), т.е. «сдвинуть» вычисления на 1 период раньше (см. файл примера).Функция ПРОЦПЛАТ() начисленные проценты за пользование кредитом указывает с противоположным знаком, чтобы отличить денежные потоки (если выдача кредита – положительный денежный поток («в карман» заемщика), то регулярные выплаты – отрицательный поток «из кармана»).

Расчет суммарных процентов, уплаченных с даты выдачи кредита

Выведем формулу для нахождения суммы процентов, начисленных за определенное количество периодов с даты начала действия кредитного договора. Запишем суммы процентов начисленных в первых периодов (начисление и выплата в конце периода):ПС*ставка(ПС-ПС/кпер)*ставка(ПС-2*ПС/кпер)*ставка(ПС-3*ПС/кпер)*ставка…Просуммируем полученные выражения и, используя формулу суммы арифметической прогрессии, получим результат.=ПС*Ставка* период*(1 — (период-1)/2/кпер)Где, Ставка – это процентная ставка за период (=годовая ставка / число выплат в году), период – период, до которого требуется найти сумму процентов.Например, сумма процентов, выплаченных за первые полгода пользования кредитом (см. условия задачи выше) = 150000*(12%/12)*6*(1-(6-1)/2/(2*12))=8062,50р.За весь срок будет выплачено =ПС*Ставка*(кпер+1)/2=18750р.Через функцию ПРОЦПЛАТ() формула будет сложнее: =СУММПРОИЗВ(ПРОЦПЛАТ(ставка;СТРОКА(ДВССЫЛ(«1:»&кпер))-1;кпер;-ПС))

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

А = К * S

где:

• А – сумма платежа по кредиту;
• К – коэффициент аннуитетного платежа;
• S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

• где i – процентная ставка за месяц, результат деления годовой ставки на 12;
• n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
2. Составим график погашения кредита. Пока пустой.
3. В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.

Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

• сумма основного долга распределена по периодам выплат равными долями;
• проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

где:

• ДП – ежемесячный платеж по кредиту;
• ОСЗ – остаток займа;
• ПП – число оставшихся до конца срока погашения периодов;
• ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

Составим график погашения займа:

Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Примеры расчетов регулярных платежей по аннуитетной схеме в Excel

Функция ОСПЛТ используется для расчетов задолженностей по аннуитетной схеме. То есть, сумма платежа за каждый период состоит из тела кредита (основной суммы задолженности) и процентов (части средств, которые выплачивают сверху за использование финансового продукта). Процентная ставка является неизменной величиной. Соотношение процентной части к телу кредита в каждом периодическом платеже меняется со временем. Рассматриваемая функция позволяет определить сумму основной задолженности (без учета процентов), выплаченной в определенный период согласно графику.

Пример 1. Банк выдал кредит на сумму 10 000 руб. под 18% годовых сроком на 1 год. Был составлен график ежемесячных выплат. Определить, какую сумму тела кредита выплатит клиент в 3-1 месяц.

Вид таблицы данных:

Для расчета используем следующую функцию:

=ОСПЛТ(B3/12;3;B4;B5)

Описание аргументов:

• B3/12 – размер ставки, приведенной к числу периодов выплат (12 месяцев);
• 3 – номер периода, для которого выполняется расчет;
• B4 – общее число периодов (12 месяцев в году);
• B5 – сумма кредита по договору.

Результат вычислений:

Полученное значение – отрицательное число, поскольку оно отражает расходы клиента по оплате финансового продукта.

Недостатки калькулятора

1. Нет учета возможное изменение процентной ставки во время выплат кредита
2. Если сделать расчет, делая досрочные платежи в изменение срока и суммы, то расчет будет неверным
3. Если сумма процентов, начисленных за период больше суммы аннуитетного платежа, то расчет будет не верным
4. Не рассчитывается вариант — первый платеж только проценты. В случае когда дата выдачи не совпадает с датой первого платежа, вам нужно будет заплатить проценты банку за период между датой выдачи и датой первого платежа.
5. Расчет производится для процентой ставки с 2мя знаками после запятой.

Всех выше названных недостатков лишен кредитный калькулятор для iPad/iPhone. В целом недостатки не сильно критичны и они присущи любому кредитному калькулятору онлайн. Другой кредитный калькулятор в Excel можно скачать по данной ссылке. Данный кредитный калькулятор не позволяет рассчитать досрочное погашение. Однако его плюс в том, что он рассчитывает кредит с несколькими процентными периодами. Если сумма процентов по кредиту за данный месяц больше суммы аннуитетного платежа, то график для первого кредитного калькулятора в excel строится некорректно. В графике получаются отрицательные суммы.

Попробуйте посчитать к примеру кредит 1 млн. руб под 90 процентов на срок 30 лет. У второго калькулятора нет данного недостатка. Однако он делит кредит на 2 периода, т.е. возможно что после деления в графике снова будут отрицательные значения. Тогда график платежей нужно делить на 3 и более периода. Естественно сам файл также можно отредактировать под свои нужды.

Основная формула аннуитетного платежа в Excel

Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:  

Основные значения формулы расшифровываются так:

• АП – аннуитетный платеж (название сокращено).
• О – размер основного долга заемщика.
• ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
• С – число месяцев, на протяжении которых длится кредитование.

Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.

Примеры использования функции ПЛТ в Excel

Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:

1. Составить общую таблицу в Excel по исходным данным.

Таблица, составленная по условию задачи. В действительности можно задействовать другие столбцы для ее размещения

1. Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
2. В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
3. В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
4. Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».

Необходимые действия в окне «Аргументы функции». Здесь указан порядок заполнения каждого параметра

1. Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».

Финальный результат. Ежемесячный платёж посчитан и выделен красным цветом

Пример расчета суммы переплаты по кредиту в Excel

В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:

1. Составить исходную таблицу данных.

Таблица, составленная по условию задачи

1. Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
2. В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.

Финальный результат. Практически двукратная переплата

Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:

1. Составить табличку по исходным данным.

Таблица, составленная по данным из условия задачи

1. В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
2. Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.

Окончательный результат расчета

Особенности использования функции ПЛТ в Excel

В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; ; ). У функции есть следующие особенности:

Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.

Пример расчета аннуитетного кредита с досрочными платежами

Теперь давайте попробуем рассчитать ипотеку. Для примера возьмем займ со следующими параметрами

Параметры рассчитываемого кредита
Сумма	1 млн рублей.
Ставка	12%
Срок	60 месяцев
Дата первого платежа	1 сентября 2011.

где Погашение ОД — сумма в погашение тела займа
Проценты — сумма процентов по ссуде за месяц.
Где сумма ОД — сумма основного долга на дату расчета.Ставка — процентная ставка в текущем периоде. Если было изменение процентной ставки, берется новая ставка.Число дней между датами — разность в днях между датами «Дата текущего платежа» и дата предыдущего платежа.
Число дней в году — целое число дней в текущем году. Если мы считаем процентный платеж к примеру с 22 декабря 2011 по 22 января 2012 то формула процентов имеет вид.
Т.е.нужно посчитать отдельно проценты за декабрь и за январь в зависимости от числа дней в году.

В нашем примере при первом платеже это делать не нужно.
Рассчитаем первый платеж в уплату процентов по указанному выше займу за сентябрь месяц(разнца между датами 31 день).
Как видно сумма ОД на первый месяц составляет 1 млн. рублей. Подставим даты, ставки и число дней в году.

Как видно, в счет уплаты процентов должно пойти 10191.78
Произведем расчет суммы в погашение тела займа

Теперь рассчитаем сумму основного долга после оплаты первого взноса по ипотеке

Далее проценты будут начисляться на данную сумму. Так можно посчитать график для всех платежей.
Из графика платежей видно, что сумма основного долга на 1 сентября 2012 года составляет 831206.27 рублей.

Теперь допустим, мы погасили 100000 рублей в августе 2012. Тип погашения — в уменьшение суммы займа. Т.е срок останется тем же, а ежемесячный платеж уменьшится.
Попробуем посчитать, сколько будет составлять платеж после учета досрочных погашений. В октябре будет уже новый платеж по займу с учетом досрочки.

Воспользуемся формулой для расчета аннуитетных платежей. Из всех параметров у нас изменилась только сумма основного долга после досрочного погашения в августе она равна

Вычисленная выше сумма и будет сумма кредита после досрочного погашения.
Именно исходя из этой суммы и будет рассчитываться ежемесячный аннуитетный платеж после досрочного погашения.

Очевидно срок кредита также изменится, нужно отнять от общего срока число месяцев, прошедшее до досрочного погашения с момента выдачи займа.

Подставим новую сумму в формулу аннуитетного платежа получим новый платеж по займу.

Вот как выглядят промежуточные расчеты

Итоговый расчет

Проверим это с помощью программы кредитный калькулятор

Как видно результат полностью совпадает. Также можно воспользоваться онлайн версией кредитного калькулятора. Там используется указанная выше формула аннуитетного платежа. График кредитного калькулятора может быть использован для сверки расчетов вашего кредита с расчетом банка. Иногда данные могут не совпасть.

Features and benefits

SpreadsheetConverter is the perfect tool for creating calculating web forms and web pages that attract attention.

• Instantaneous response: All calculations and validations are done immediately when the user enters new data. Everything is done in the browser. No communication with the web server.
• Everything is live and interacting with your visitors: The calculator or form updates dynamically when values are changed. Even the charts are live and allow users to focus on the data they are most interested in. Use calendars to select dates, stars to set ratings and sliders to vary data in real-time. Create forms with dropdown menus, checkboxes, radio buttons, large text fields, list boxes in a breeze. Design step-by-step wizards for complex forms.
• It looks so good on the web: Normally, it takes a lot of time to make a web page look this well-designed. With Excel you just format the page the way you like. SpreadsheetConverter creates a web page that looks the same: borders, colors, fonts, checkboxes, dropdown lists etc work as they should, and numbers are formatted on the fly with decimals, thousand separators and currency symbols. Conditional formatting makes the most important numbers stand out. Design colorful themes the give your online spreadsheets a common look.
• Built-in web publishing. The Publish to Cloud feature instantly publishes your converted web pages on distributed Amazon S3 web servers for rapid global deployment.
• You get a free WordPress plugin that imports converted Excel spreadsheets into WordPress. Create live calculators and smart web form and display them in your pages or posts.
• All devices supported: the calculator or web form automatically adapts to the small screen in a smartphone or tablet, to look and work well on any device.
• Integrates with existing systems in many ways, e.g. sends data with barcodes, http or e-mail; receives data via http.
• Two or more team members can share the same spreadsheet: your users can collaborate with colleagues in real-time directly inside the web page.
• The Link Image widget allows you to show different images on the web page depending on cell values or formulas. Now you can build advanced imaging applications where an image on the screen changes with the values in a web form or calculator.

Как рассчитать аннуитетный платеж в Excel

Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.

Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.

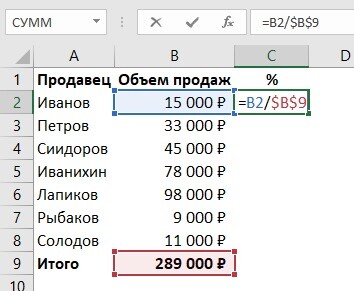
Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:

Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.

Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:

Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:

Здесь нам требуется заполнить три поля:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12.
• «Кпер» – общий срок кредитования.
• «Пс» – сумма кредита (указывается со знаком минус).

Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус

Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.

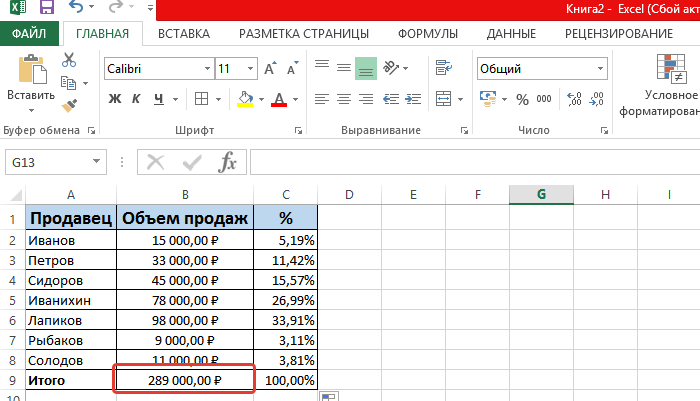
После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:

Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.

Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках

Можно было просто вписать в строке формул то, что там сейчас вписано

По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.

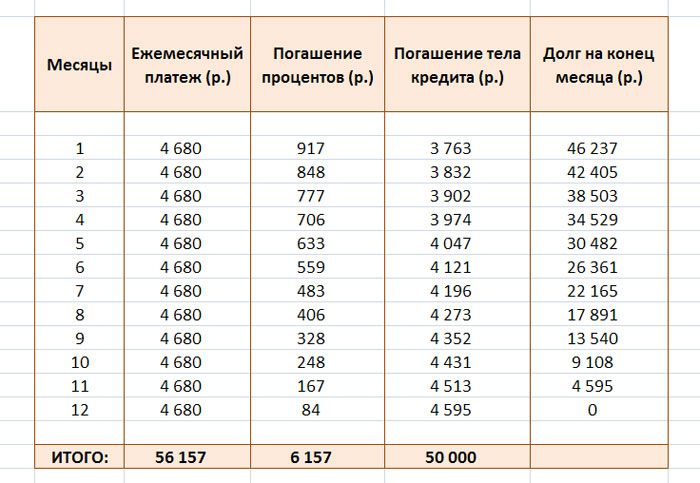
Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:

На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.

Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.

Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.

Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:

Расчет в Excel суммы кредита для заданного аннуитетного платежа

В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей. По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.

Что же, друзья, не будем терять время! Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!

Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами. Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.

Чтобы рассчитать сумму ожидаемого кредита надо воспользоваться функцией ПС, предварительно кликнув по ячейке, в которой мы хотим видеть свой расчёт (в нашем калькуляторе это ячейка с координатой C11). Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12 (в нашем случае: C5/12).
• «Кпер» – общий срок кредитования (в нашем калькуляторе, это ячейка с координатой C6).
• «Плт» – ежемесячный аннуитетный платёж, перед которым ставим знак минус (в нашем калькуляторе, это ячейка C4, перед данной координатой мы и ставим знак минус).

Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.

Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4)

Те самые параметры, которые мы вводили в таблице функции ПС.

Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:

• Общая сумма выплат – это ежемесячный аннуитетный платёж (ячейка С4) умноженный на общий срок кредитования (ячейка С6). В строку формул вводим следующие данные: =C4*C6.
• Переплата (проценты) по кредиту – это общая сумма выплат (ячейка С12) минус сумма кредита (ячейка С11). В строку формул записываем: =C12-C11.
• Эффективная процентная ставка (или полная стоимость кредита) – это общая сумма выплат (ячейка С12) делённая на сумму кредита (ячейка С11) и минус единица. Затем всё это делим на срок кредитования, выраженный в годах (ячейка C6 делённая на 12). В строку формул записываем: = (C12/C11-1)/(C6/12).

Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования. Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:

Чем хорош и плох аннуитет?

Хотя аннуитетный платёж выгоден банку, для клиента тут тоже есть свои положительные стороны.

Основной плюс – погашение происходит небольшими суммами. Это снимает чрезмерную финансовую нагрузку на бюджет гражданина. Обычно за кредитами обращаются те частные лица, кто не располагает возможностью тратить большие объёмы средств, так что для них важен момент размера выплат.

При этом обратите внимание, что выше мы уже показали, сколько переплачивает заёмщик при аннуитете. Если посмотреть на окончательную стоимость займа, становится понятно, как много теряет обыватель

Это очень серьёзный минус.

В свете обозначенных в статье сведений всё же нельзя сказать, что дифференцированная форма погашения кредита однозначно лучше. Такая схема выплат подразумевает погашение сразу через большие суммы, что обычно себе не могут позволить обыватели.

Каждый клиент должен сам решить для себя, как ему выгоднее рассчитываться с кредитно-финансовым учреждением: медленно, но менее болезненно с денежной точки зрения, или быстро, но с существенной нагрузкой на бюджет.

Аннуитетный платёж – это про “медленно и почти безболезненно”.

Формы покрытия кредита

Такой серьёзный вопрос, как порядок возвращения заёмных средств, всегда оговаривается кредитно-финансовыми учреждениями заранее. Лишь после разъяснения всех нюансов клиенту кредит предоставляют в пользование.

Существует всего две формы погашения займа:

• дифференцированный платёж;
• аннуитетный платёж.

Большая часть заёмщиков по понятной причине в первую очередь обращает своё внимание на процентную ставку. Как правило, этот параметр является ключевым для среднестатистического обывателя, т.к

его воспринимают главным в вопросе определения объёма переплаты.

Однако также есть фактор способа начисления процентов и покрытия займа. Эти два обстоятельства оказывают не меньшее влияние на то, во сколько в итоге обойдётся кредит.

Примечание 1. Считается, что наиболее выгодной формой выплаты задолженности является дифференцированный платёж. В рамках данного способа погашения займа клиент банка покрывает сразу и тело кредита, и начисляемые проценты. За счёт этого каждый месяц выплаты сокращаются, т.к. проценты начисляются на постоянно уменьшающуюся сумму.

Выплата одновременно и самого долга, и процентной ставки, безусловно выгодна пользователю банковских услуг. Однако на практике сами кредитно-финансовые учреждения продвигают второй упомянутый нами способ покрытия кредита. Почему? Потому что они стремятся зарабатывать. Аннуитетный платёж подходит в этом случае лучше всего.

Это интересно: Работа кредитным специалистом — что нужно знать