Как сделать знак приблизительно равно

Ход урока

2. Основная часть:

Учитель:А совершим мы с вами сегодня полёт в неизведанное космическое пространство. Сегодня мы будем не учениками, а исследователями космического пространства. А чтобы полёт прошёл удачно давайте вспомним, чем мы занимаемся на уроках математики?

Ученики: Решаем, считаем, пишем, думаем…

Учитель: А как вы думаете, что мы будем делать сегодня?

Учитель: Чтобы полёт прошёл удачно, необходимо быть:

• Внимательными
• Точно и правильно выполнять задания
• Не допускать ошибок, иначе ракета может потерпеть аварию.

Учитель:
Итак, повышенное внимание! До старта ракеты осталось 10 секунд, давайте немного посчитаем. (Ученики ведут счёт)

• Счёт цепочкой до 10.
• Начинает учитель, дети продолжают.
• Отсчёт в обратном направлении.
• Отсчитываем секунды 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 пуск. Мы в полёте!

Учитель: Ребята, посмотрите на доску, она сегодня превратилась в «звёздное небо». Но какие необычные звёзды! Что они нам напоминают?

Ученики: геометрические фигуры.

Учитель: Что это за фигуры, назовите.

Ученики: отрезок, прямая, точки, ломаная, кривая.

Учитель: Пока мы смотрели на небо глазки устали, давайте сделаем для них зарядку.

Учитель: Ребята, посмотрите, наш пульт управления находится в аварийном состоянии. Запали кнопки, необходимо исправить пульт.

• Какое число идёт при счёте за числом 3, 6, 9?
• Какое число стоит перед числом 2, 5, 8, 10?
• Назовите соседей числа 2, 7?

Но на пульте кроме цифр есть ещё различные знаки, они тоже стёрлись, давайте их восстановим (дети по очереди отвечают, остальные хлопают в ладоши, если верно)

2 3=5		4 =2
5 1=4		1+ =4
3+ =5		5- =4

Молодцы! Пульт исправен.

Учитель: Пока наша ракета поднимается ввысь, поиграем в игру «Сложи фигуру».

Нужно из палочек сложить фигуру, состоящую из четырёх квадратов.

Посчитай сколько здесь квадратов? (фигура состоит из 4 квадратов)

Переложи 2 палочки так, чтобы получилось 5 одинаковых квадратов.

Физминутка: (негромко звучит весёлая музыка)

Учитель: А сейчас приготовьте свои квадраты. Положите в верхний ряд 2 зелёных квадрата, а в нижний 3 синих.

Каких квадратов меньше?

Какое число меньше 2 или 3?

В математике есть специальная запись. Это записывают так: 2

Каких квадратов больше? (синих)

Какое число больше? (3)

Кто догадался, как это записать? 3>2

> – знак больше

Знак ставится так, чтобы к большему числу «клювик» был открыт.

Давайте отдохнём и посмотрим телевизор, что у нас сегодня показывают (работа с учебником, выполнение задания).

• Сколько было птичек на первой картинке
• Сколько прилетело
• Сколько стало
• Их стало больше или меньше
• Как это записали, прочитайте
• Сколько ягод на кисточке
• Что произошло с ягодами
• Как это записать
• Какое число больше, меньше?

Учитель: Наша ракета стремительно несётся ввысь. Экипаж работает слаженно, чётко. Сейчас серьёзная работа, мы выходим в открытый космос. О, я вижу планету, от неё отделяется какой-то неожиданный летающий объект. Что это? Инопланетяне хотят уничтожить нашу ракету. Приготовьтесь к математическому сражению. А оружием будет ум и смелость. Я показываю пример, вы с помощью веера цифр ответ.

У кого можно попросить помощи, если очень трудно? (соседа по парте)

2+2		1+2		4-2
3+2		3-1		5-3

– Мы победили, корабль удаляется. Заполним ботржурналы. Проверьте рабочее место, сядьте поудобнее, чтобы бортжурналы лежали правильно, записи были чёткими и аккуратными. Работаем на странице 11. (работа в тетрадях на печатной основе для 1 класса)

– Перед вами знаки. Как называется первый знак? (больше)

Как называется второй знак? (меньше)

Напишите знак по точкам, допишите до конца строки.

Учитель: Перед стартом ракеты я предлагаю вам поработать в паре. У вас на столах карточки, нужно вставить недостающие знаки «больше» или «меньше».

Карточка.

2*3		5*7		8*5
5*3		10*7		6*2
3*9		7*1		6*9

3. Рефлексия:

Благодаря дружной работе наша ракета совершила мягкую посадку. Во время полёта мы провели большую работу.

– Скажите, что вы для себя узнали нового?

– Чем мы сегодня занимались?

– Что вам помогло хорошо работать на уроке?

У вас на столах лежат мордочки, нарисуйте на них выражения лица весёлое или грустное, кому на уроке было хорошо поднимите весёлую мордочку. А у кого что-то не получилось и было грустно? (таких может не быть)

Полёт завершён, всем спасибо!

ТБ(1) — это ставка на то, что общее количество голов в матче будет больше 1.

Тотал 1б не обязательно может быть на количество голов в футбольном матче, его могут применять как к разным видам спорта, так и к разным событиям, например: угловые, желтые карточки и т.д.

Также букмекеры дают доп тоталы, к примеру можно поставить на «тотал 1 тайма больше 1»

Это значит что вы ставите на то, что в первом тайме будет забито больше 1 гола.

Типы неравенств

1. Строгие неравенства — используют только знак больше (>) или меньше (<).

• a < b — это значит, что a меньше, чем b.
• a > b — это значит, что a больше, чем b.
• неравенства a > b и b < a означают одно и тоже, то есть равносильны.

1. Нестрогие неравенства — используют знаки сравнения ≥ (больше или равно) или ≤ (меньше или равно).

• a ≤ b — это значит, что a меньше либо равно b.
• a ≥ b — это значит, что a больше либо равно b.
• знаки ⩽ и ⩾ являются противоположными.

1. Другие типы неравенств.

• a ≠ b — означает, что a не равно b.
• a ≫ b — означает, что a намного больше, чем b.
• a ≪ b — означает, что a намного меньше, чем b.
• знаки >> и << противоположны.

Развивать математическое мышление детей помогут уроки математики в школе Skysmart. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой и влюбиться в числа.

Запишите вашего ребенка на бесплатное пробное занятие в Skysmart: поиграем в цифры вместе с енотом Максом и покажем, что математика — это очень увлекательно!

Alt-коды в помощь

Как поставить знак «Примерно равно» на клавиатуре? Как уже было сказано, пользователь не сможет ни при каких обстоятельствах отыскать соответствующий элемент на клавиатурной панели. Зато при желании можно без труда напечатать его посредством специализированных команд и кодов. Начнем с самого простого. Речь идет об Alt-кодах. Их иногда называют ASCII-кодами. С помощью специальных комбинаций продвинутые ПК-пользователи печатают различные уникальные символы. И знаки приблизительного равенства не являются исключением.

Чтобы осуществить их вставку в текст, потребуется:

Дело сделано. Символ «Примерно равно» будет установлен в указанном заранее месте. Подобный расклад на практике встречается все чаще. Он значительно упрощает жизнь продвинутым юзерам.

Важно: на клавиатуре можно увидеть разные кнопки «Альт». При работе с ASCII-кодами необходимо воспользоваться одной из соответствующий клавиш

Не важно, с какой стороны клавиатуры.

Ставим символы, которых нет на клавиатуре

Вариант 1: Word и его аналоги

Если у вас на компьютере установлена современная версия Word — то найти большинство самый популярных символов проще простого!

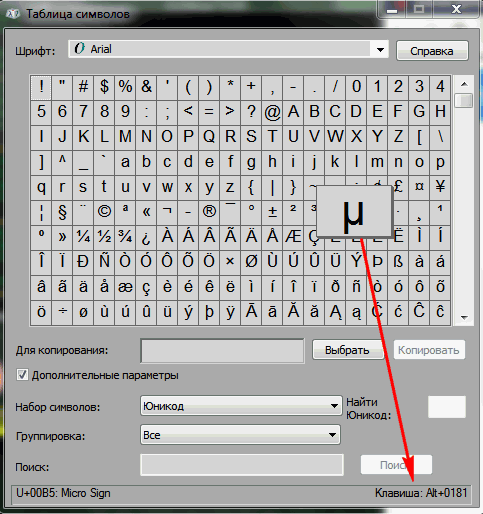
Необходимо зайти в меню «Вставка/Символы/Символы» (см. пример на скриншоте ниже ).

Если на рабочем ПК MS Office нет — хорошим вариантом может стать сервис Яндекс-Диск (прим.: там есть встроенная онлайн-версия Word). Меню выглядит аналогично вышеприведенному.

Яндекс-Диск — создать Word-документ

Кстати, как еще одной неплохой и бесплатной альтернативой Office — могу порекомендовать пакет LibreOffice. Вместо Word там используется редактор Writer.

Запустив эту программу и зайдя в меню «Вставка / Специальные символы» — вы найдете тысячи всевозможных знаков.

Writer — вставка символов

Вариант 2: готовая табличка с популярными знаками

У меня есть подготовленная небольшая табличка () со всеми самыми нужными символами: она покрывает 98% всех популярных офисных задач.

Рекомендую вам ее скопировать к себе во вспомогательный документ Word, и когда понадобиться какой-нибудь символ — просто выделить его и скопировать из нее (сочетание для копирования: Ctrl+C; для вставки: Ctrl+V).

Источник

Неправильное использование

Знак равенства иногда используется неправильно в математических аргументах для нестандартного соединения математических шагов, а не для демонстрации равенства (особенно ранними математиками).

Например, если кто-то шаг за шагом находит сумму чисел 1, 2, 3, 4 и 5, можно неправильно написать:

1 + 2 = 3 + 3 = 6 + 4 = 10 + 5 = 15.

Структурно это сокращение для:

( + 4 = 10) + 5 = 15,

но обозначение неверно, потому что каждая часть равенства имеет разное значение. Если интерпретировать строго так, как говорится, это будет означать, что

3 = 6 = 10 = 15 = 15.

Правильная версия аргумента была бы такой:

1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15.

Эта трудность возникает из-за тонких различий в использовании знака в образовании. В ранних оценках, ориентированных на арифметику, знак равенства может быть рабочим ; подобно кнопке равенства на электронном калькуляторе, он требует результата вычисления. Начиная с курсов алгебры, этот знак приобретает относительный смысл равенства между двумя вычислениями. Путаница между двумя способами использования знака иногда сохраняется на университетском уровне.

Кавычки ёлочки. Когда, зачем и как сделать

Кавычки ёлочки – парный знак препинания, который используется в определённых случаях. Поэтому встречается далеко не во всех текстах.

Кавычки ёлочки на экране будут выглядеть так – «». И поставить их с помощью клавиатуры не составит никакого труда.

Второе название кавычек этого типа – французские. Связано это с тем, что использовать их стали с лёгкой руки Гийома Ле Бе. Это был известный в своё время гравёр, который специализировался на еврейских шрифтах.

Как поставить кавычки ёлочки

Многие задают себе такой вопрос – как сделать кавычки ёлочки? Оказывается, ответ на него получить не так просто. И здесь всё зависит от того, где именно вы хотите поставить этот парный знак.

Давайте разберём самые популярные случаи, а заодно узнаем, как ставить кавычки ёлочки.

Кавычки ёлочки в Word

Чтобы поставить кавычки в Ворде, следует первым делом проверить, чтобы раскладка клавиатуры соответствовала русскому языку.

Теперь надо нажать на кнопочку SHIFT.

Не отпуская SHIFT нажать в верхней строке на цифру 2. И вы тут же получите свои первые открывающиеся кавычки – ёлочки. Вот такие «.

Чтобы закрыть кавычки надо снова нажать на SHIFT. Затем на кнопочку 2 и получить закрывающуюся часть кавычек ёлочек. Вот такую – ».

Открою маленький секрет. Чтобы не проводить эту процедуру по два раза можно за одно нажатие SHIFT установить сразу и открывающуюся и закрывающуюся часть кавычек, а после просто в готовых ёлочках вписать текст, установив курсор между ними.

Вывод: как поставить кавычки ёлочки на клавиатуре? Для этого необходимо знать сочетание клавиш «SHIFT + 2».

Кавычки ёлочки в Excel

Как в Ворде поставить кавычки ёлочки стало понятно. Но как получить этот же знак в Excel? Здесь есть два варианта.

В первом случае можно всего лишь скопировать необходимый знак всё с того же Ворда и вставить в нужную часть документа Excel.

Второй, с использованием кода, рассмотрим ниже.

Кавычки ёлочки в Photoshop

Символ кавычки ёлочки может пригодиться и при работе с Photoshop. Установить их здесь можно точно так же, как и в варианте с Excel, то есть просто скопировать и вставить.

Да простят меня гуру и асы Photoshop…

Кавычки ёлочки на ноутбуке

Если в своей работе вы используете ноутбук, то поставить в тексте необходимый знак очень просто.

• Перевести клавиатуру на русскую раскладку.
• Нажать кнопку SHIFT.
• Нажать на клавишу с цифрой 2 два раза, чтобы сразу поставить и открывающиеся, и закрывающиеся ёлочки.

Всё, работа сделана. Осталось только вписать тот самый закавыченный текст.

Ёлочки кавычки. Какие ещё можно использовать клавиши

Есть довольно распространённый способ написать символ кавычки ёлочки. Для этого на клавиатуре надо одновременно нажать такие клавиши ALT + 0171 (открывающие) или 0187 (закрывающие). Данный метод подходит абсолютно для любого редактора.

Теперь следует нажать ALT и поочерёдно нажимать на клавиши 0171 для открывающихся ёлочек или 0187 для закрывающихся. После каждого набранного кода клавишу  ALT надо отпустить.

Когда надо ставить кавычки ёлочки

Русские кавычки ёлочки, а называются они так потому, что выполняются на русской раскладке клавиатуры, используются для цитат, названий литературных произведений, названий газет, журналов, предприятий и много ещё для чего.

Примеры:

• Газета «Пламя» выходит раз в неделю.
• Наш теплоход «Иванов» прибывает сегодня.
• Недавно я читала роман Льва Толстого «Война и мир» (на самом деле читала, и даже дочитала до самого конца).

Но что делать, если в тексте, который написан в кавычках ёлочках надо написать ещё один закавыченный текст?

Но это тема для другой статьи.

Ёлочки и лапки в Яндекс Дзен

Не так давно в Яндекс Дзен, а точнее в их группе ВКонтакте поднималась тема ёлочек и лапок. Было объявлено, что авторы должны быть грамотны и писать кавычки ёлочки и лапки в правильных местах. И ни в коем случае не путать эти два разных знака.

Видимо теперь здесь будут блокировать каналы и за то, что вы случайно перепутаете ёлочки и лапки в своём тексте.

Кстати, именно эта тема, поднятая в Дзене, вдохновила меня на эту статью. Надеюсь, она окажется вам полезной.

Наиболее частые

Alt + 0160: неразрывный пробел Alt + 255: неразрывный пробел

– Alt + 0150: короткое тире — Alt + 0151: длинное тире … Alt + 0133: многоточие « Alt + 0171: левые кавычки «ёлочки» » Alt + 0187: правые кавычки «ёлочки» у́же Alt + 0769: знак ударения § Alt + 0167: параграф

Alt + 126: тильда Alt + 92: обратная косая черта ° Alt + 0176: градус (угол или температура) ± Alt + 0177: плюс/минус ≤ Alt + 8804: меньше/равно ≥ Alt + 8805: больше/равно ≈ Alt + 8776: примерно равно ≠ Alt + 8800: не равно ² Alt + 0178: вторая степень ³ Alt + 0179: третья степень × Alt + 0215: знак умножения ÷ Alt + 0247: знак деления (обелюс)

£ Alt + 0163: фунт стерлингов € Alt + 0128: евро ¥ Alt + 0165: японская иена Alt + 0169: копирайт Alt + 0174: зарегистрированная торговая марка Alt + 0162: торговая марка

При отсутствии блока цифровой клавиатуры, например на нетбуках, необходимо её включить сочетанием клавиш Fn и F11 или, при наборе дополнительно удерживать клавишу Fn . Для набора цифр Alt-кода на нетбуках используются функциональные клавиши.

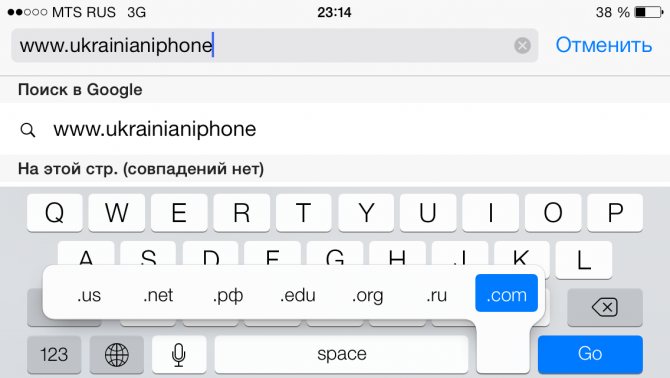
На клавиатуре отсутствует знак приблизительного равенства, а для вставки часто применяют копирование из другого места. Но есть и более удобные способы, которые помогут быстро напечатать символ в любом месте документа word или excel.

Готовые символы

Знак «Примерно равно» на клавиатуре найти не получится. Дело все в том, что этот символ является специальным. Клавиатурную панель можно использовать для печати примерного равенства, но далеко не всегда.

Иногда упомянутый элемент текстового документа проще скопировать и ставить в нужное место. Действовать предлагается таким образом:

1. Отыскать текст, где есть знак волнистого равно. Это и есть приблизительное равенство.
2. Выделить его любым известным способом.
3. Нажать Ctrl + C либо ПКМ + «Копировать».
4. Поставить курсор в место предполагаемой печати.
5. Зажать Ctrl + V либо ПКМ + «Вставить».

Проделанные действия помогут быстро напечатать скопированный в буфер обмена специальный знак

Этот подход используется не слишком часто, но помнить о нем крайне важно

Связанные символы

Примерно равно

Символы, используемые для обозначения примерно одинаковых предметов, включают следующее:

• ≈ ( U +2248, LaTeX \ приблизительно )
• ≃ (U + 2243, LaTeX \ simeq ), комбинация ≈ и =, также используется для обозначения асимптотического равенства
• ≅ (U + 2245, LaTeX \ cong ), еще одна комбинация ≈ и =, которая также иногда используется для обозначения изоморфизма или конгруэнтности
• ∼ (U + 223C, LaTeX \ sim ), который также иногда используется для обозначения пропорциональности или сходства , связанных отношением эквивалентности , или для обозначения того, что случайная величина распределена согласно определенному распределению вероятностей (см. Также тильду )
• ∽ (U + 223D, LaTex \ backsim ), который также используется для обозначения пропорциональности
• ≐ (U + 2250, LaTeX \ doteq ), который также может использоваться для представления приближения переменной к пределу
• ≒ (U + 2252, LaTeX \ Falldotseq ), обычно используется в Японии , Тайване и Корее .
• ≓ (U + 2253, LaTex \ risedotseq )

Не равный

Символ , используемый для обозначения неравенстве (когда элементы не равны) является полоснул знак равенства ≠ (U + 2260). В LaTeX это делается с помощью команды «\ neq».

Большинство языков программирования, ограничивая себя в 7-битным ASCII набор символов и печатаемые символы , использование , , или представлять их логический оператор неравенства .

Личность

Тройника символ ≡ (U + +2261, латексные \ эквив ) часто используется для обозначения идентичности , а определение (которое также может быть представлена U + 225D ≝ РАВНО по определению или U + 2254 ≔ ДВОЕТОЧИЕ РАВНО ), или отношение конгруэнтности в модульной арифметике .

Изоморфизм

Символ ≅ часто используется для обозначения изоморфных алгебраических структур или конгруэнтных геометрических фигур.

В логике

Равенство значений истинности (посредством двойного импликации или логической эквивалентности ) может обозначаться различными символами, включая = , ~ и ⇔ .

Другие связанные символы

Дополнительные символы в Юникоде, связанные со знаком равенства, включают:

• ≌ ( U + 224C ≌ ВСЕ РАВНО )
• ≔ ( U + 2254 ≔ COLON EQUALS ) (см. Также задание (информатика) )
• ≕ ( U + 2255 ≕ РАВНО ДОЛЖНА )
• ≖ ( U + 2256 ≖ КОЛЬЦО РАВНО )
• ≗ ( U + 2257 ≗ КОЛЬЦО РАВНО )
• ≘ ( U + 2258 ≘ СООТВЕТСТВУЕТ )
• ≙ ( U + 2259 ≙ ОЦЕНКИ )
• ≚ ( U + 225A ≚ РАВНОМЕРНО )
• ≛ ( U + 225B ≛ ЗВЕЗДНЫЕ РАВНЫ )
• ≜ ( U + 225C ≜ ДЕЛЬТА РАВНА )
• ≞ ( U + 225E ≞ ИЗМЕРЕНО )
• ≟ ( U + 225F ≟ ВОПРОСЫ — РАВНО ).

Типография и внешний вид

Угловые скобки , символы сравнения и простые гильеметы (полукруглые символы) в шрифтах Cambria, DejaVu Serif, Andron Mega Corpus, Andika и Everson Mono

Знаки «меньше» и «больше» состоят из линии, изогнутой посередине с прямыми участками, при этом угол перегиба обычно острый (то есть меньше прямого). Концы перпендикулярны друг другу, чтобы ноги были равной длины; в основном это выделено курсивом . Высота и положение знаков обычно соответствуют положению знака плюс . Поэтому в большинстве шрифтов они значительно больше, чем Guillemets (заостренные символы), и, с другой стороны, значительно меньше, чем угловые скобки . Последние также отличаются тем, что у них гораздо более открытый угол на изгибе, в большинстве случаев намного больше, чем прямой угол.

Как получить буквы с диакритическими знаками в Microsoft Word?

Обновлено: 30.12.2019 компанией Computer Hope

Для пользователей, у которых нет специальной клавиатуры, буквы с диакритическими знаками могут быть созданы только с помощью сочетаний клавиш или через строку меню.

Вставка букв с диакритическими знаками с помощью строки меню или ленты

Если вы вставляете акцентированный символ, используя описанные выше шаги, после вставки символа вы можете скопировать этот символ и вставить его в любое другое место в документе.

Используйте сочетания клавиш

После отпускания сочетания клавиш необходимо быстро нажать буквенную клавишу. В противном случае создается буква без ударения.

Чтобы получить прописные буквы с диакритическими знаками, обязательно включите Caps Lock до с помощью сочетаний клавиш. В качестве альтернативы, после одновременного нажатия сочетаний клавиш отпустите все клавиши, кроме клавиши Shift, а затем нажмите нужную букву, чтобы создать заглавную букву с ударением. Параметр клавиши Shift работает только для тех сочетаний клавиш, в которых используется клавиша Shift, как указано ниже.(каретка), буква

ã, ñ, õ, Ã, Õ, Õ Ctrl + Shift +

(тильда), буква

ä, ë, ï, ö, ü, ÿ, Ä, Ë, Ï, Ö, Ü, Ÿ Ctrl + Shift +: (двоеточие), буква

М, Е (At), a или A

æ, Ctrl + Shift + & (амперсанд), a или A

œ, Œ Ctrl + Shift + & (амперсанд), o или O

ç, Ç Ctrl +, (запятая), c или C

ð, Ð Ctrl + ‘(апостроф), d или D

ø, Ø Ctrl + /, o или O

¿ Alt + Ctrl + Shift +?

¡ Alt + Ctrl + Shift +!

ß Ctrl + Shift + &, s

Использование круглых скобок в математике

Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.

Первое применение.

С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.

Например, выражение $2+3cdot 2$ не равносильно выражению $(2+3)cdot 2$. Для первого выражения сначала вычисляется произведение, а затем сумма, для второго же выражения сначала вычисляется сумма, так как она стоит в скобках, и лишь затем произведение.

В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.

Готовые работы на аналогичную тему

Второе применение.

Скобками выделяют отрицательные числа в выражениях для того чтобы избежать путаницы. Например, выражение $(-5) cdot 2 + (3 cdot 12)$. Однако, если отрицательное число стоит в выражении на первом месте, оно может и не выделяться скобками.

Третье применение.

Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.

$(x+2)^2; int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$

Четвёртое применение.

Круглыми скобками обозначаются отрезки, границы которых не включены интервал. Интервал с круглыми скобками вида $(-a;+a)$ можно иначе записать как строгое неравенство вида $-a$

Пятое применение.

Скобки также используются при необходимости записи зависимости какой- либо функции от аргумента, например, $f(x)=5x+3$.

Пятое применение.

С помощью скобок записываются координаты точек, например, , запись «точка, с координатами $(1; 2)$» обозначает, что по оси абсцисс координата точки равна единице, а по оси ординат — двум.

Угловые скобки

В математике угловыми скобками обозначают кортеж, реже — скалярное произведение в предгильбертовом пространстве, например:

В квантовой механике угловые скобки используются в качестве так называемых бра и кет (от англ. bracket — скобка), введённых П. А. М. Дираком для обозначения квантовых состояний (векторов) и матричных элементов. При этом квантовые состояния обозначаются как (кет-вектор) и (бра-вектор), их скалярное произведение как матричный элемент оператора А в определённом базисе как

Кроме того, в физике угловыми скобками обозначают усреднение (по времени или другому непрерывному аргументу), например, — среднее значение по времени от величины f.

В текстологии и издании литературных памятников угловыми скобками обозначают лакуны в тексте — .

Общая характеристика

Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.

Значение и разновидности

Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.

В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||

Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания

Разновидности:

• Круглые ().
• Квадратные .
• Фигурные { }.
• Угловые ⟨ ⟩ (< > в ASCII-текстах).

В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), , { }(), , { }. Также встречаются двойные, называемые обратными (]] и [ [) или << и >> в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.

Основные цели квадратной скобки в математике:

• Взятие целой части числового значения.
• Округление до близкого знака.
• Возведение в степень, взятие производной или подсчёт подинтегрального выражения.
• Приоритет операций. Примером может быть следующий способ: 3.

Другие варианты расчета:

• Векторное произведение — с = = = a*b.
• Закрытие сегмента означает, что в множество включены цифры 1 и 2.
• Коммутатор .
• Заменяют круглые скобки при записи матриц по правилам.
• Одна [ объединяет несколько уравнений или неравенств.
• Нотация Айверсона.

Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.

Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.

На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная { встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.

Одинарные или двойные выражения

Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.

В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.

Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.

По правилам интервал записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.

Также используются в математике как круглые, так и прямые знаки, означающие, что на конце отрезка, рядом с которым имеется круглая скобка, равенство строгое, а на том, где скобка квадратная — нестрогое. Интервал (−5;5] иначе записывается неравенством $5.

В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.

В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).

Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0

Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.

Равенство и неравенство

Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.

Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».

Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.

Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.

Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн формате. Как найти знаки на клавиатуре? Ответ на картинке:

Word: изменить нумерацию заголовков с последовательной на нумерацию глав

Сценарий:

Предварительные требования:

Этот набор шагов работает ТОЛЬКО, если вы используете автоматическую нумерацию структуры для стилей заголовков. В этом сообщении не описывается, как это настроить (вместо этого см. Ссылки в этом сообщении: https://cybertext.wordpress.com/2008/09/23/word-2007-outline-numbering/).

Шаг 3. Обновите все перекрестные ссылки на рисунки и таблицы в документе

По завершении все ваши перекрестные ссылки должны отражать новую последовательность нумерации. ПРИМЕЧАНИЕ: Иногда вам нужно повторить эти шаги и обновить второй раз, чтобы все они обновились правильно.