Визуализации алгоритмов сортировки
Содержание:
- Visual Representation
- Параметр key
- Сортировка массива из случайных чисел методом пузырька
- Использовать
- Использование параметра cmp
- Code
- Пример сортировки пузыря
- Working of Bubble Sort
- Сортировка пузырьком
- Быстрая сортировка
- What is Sorting — Definition
- Сортировка слиянием
- Декорируем-сортируем-раздекорируем
- Сортировка пузырьком
- Difference between Selection, Bubble and Insertion Sort
- Analysis
- Сортировка многомерного массива
- Подробный разбор пузырьковой сортировки
Visual Representation
Given a list of five elements, the following images illustrate how the bubble sort iterates through the values when sorting them
The following image shows the unsorted list
First Iteration
Step 1)
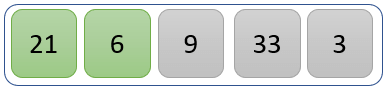
The values 21 and 6 are compared to check which one is greater than the other.
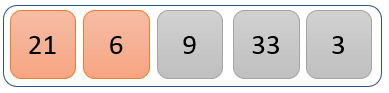
21 is greater than 6, so 21 takes the position occupied by 6 while 6 takes the position that was occupied by 21
Our modified list now looks like the one above.
Step 2)
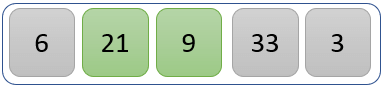
The values 21 and 9 are compared.
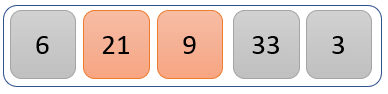
21 is greater than 9, so we swap the positions of 21 and 9
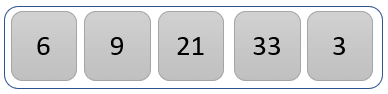
The new list is now as above
Step 3)
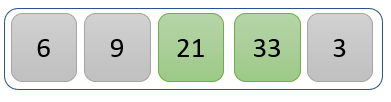
The values 21 and 33 are compared to find the greater one.
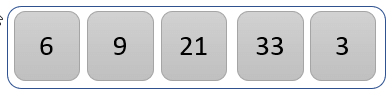
The value 33 is greater than 21, so no swapping takes place.
Step 4)
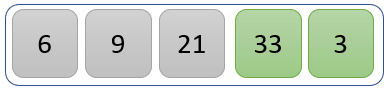
The values 33 and 3 are compared to find the greater one.
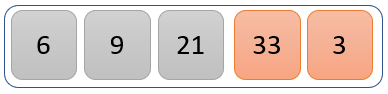
The value 33 is greater than 3, so we swap their positions.
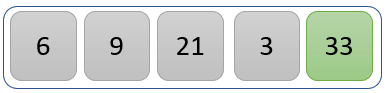
The sorted list at the end of the first iteration is like the one above
Second Iteration
The new list after the second iteration is as follows
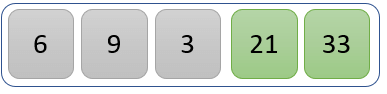
Third Iteration
The new list after the third iteration is as follows
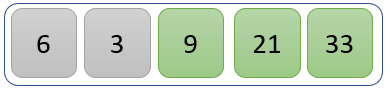
Fourth Iteration
The new list after the fourth iteration is as follows
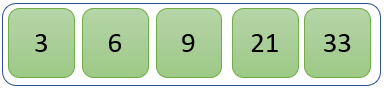
Параметр key
Функций и sorted() содержат параметр key чтобы указать функцию вызываемую для каждого аргумента перед сравнением.
Пример регистронезависимого сравнения:
>>> sorted(«This is a test string from Andrew».split(), key=str.lower)
|
1 |
>>>sorted(«This is a test string from Andrew».split(),key=str.lower) ‘a’,’Andrew’,’from’,’is’,’string’,’test’,’This’ |
Функция передаваемая в key содержит один аргумент и возвращает ключ используемый для сортировки. Это эффективный подход, так как функция вызывается ровно один раз для каждого элемента.
Общий шаблон для отсортировки сложных объектов — использование одного из индексов как ключа:
>>> student_tuples =
>>> sorted(student_tuples, key=lambda student: student) # сортировка по возрасту
|
1 |
>>>student_tuples= …(‘john’,’A’,15), …(‘jane’,’B’,12), …(‘dave’,’B’,10), >>>sorted(student_tuples,key=lambda studentstudent2)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15) |
Тот же способ работает для объектов с именованными атрибутам:
>>> class Student:
… def __init__(self, name, grade, age):
… self.name = name
… self.grade = grade
… self.age = age
… def __repr__(self):
… return repr((self.name, self.grade, self.age))
|
1 |
>>>classStudent …def __init__(self,name,grade,age) …self.name=name …self.grade=grade …self.age=age …def __repr__(self) …returnrepr((self.name,self.grade,self.age)) |
>>> student_objects =
>>> sorted(student_objects, key=lambda student: student.age) # сортировка по возрасту
|
1 |
>>>student_objects= …Student(‘john’,’A’,15), …Student(‘jane’,’B’,12), …Student(‘dave’,’B’,10), >>>sorted(student_objects,key=lambda studentstudent.age)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15) |
Сортировка массива из случайных чисел методом пузырька
Массив называется отсортированным по возрастанию, если для любых его элементов выполняется
условие a<a. Массив называется отсортированным по убыванию, если для любых его элементов выполняется условие a>a.
Существует множество методов сортировки. Одни из них являются более эффективными, другие
проще для понимания. Достаточно простой для понимания является сортировка методом пузырька, который
также называют методом простого обмена. В чем же он заключается, и почему у него такое странное
название: «метод пузырька»?
Как известно воздух легче воды, поэтому пузырьки воздуха всплывают. Это просто аналогия. В
сортировке методом пузырька по возрастанию более легкие (с меньшим значением) элементы постепенно
«всплывают» в начало массива, а более тяжелые друг за другом опускаются на дно (в конец массива).
Алгоритм и особенности сортировки:
- При первом проходе по массиву элементы попарно сравниваются между собой: первый со вторым, затем второй с третьим, следом третий с четвертым и т.д. Если предшествующий элемент оказывается больше последующего, то их меняют местами.
- Не трудно догадаться, что постепенно самое большое число оказывается последним. Остальная часть массива остается не отсортированной, хотя некоторое перемещение элементов с меньшим значением в начало массива наблюдается.
- При втором проходе незачем сравнивать последний элемент с предпоследним. Последний элемент уже стоит на своем месте. Значит, число сравнений будет на одно меньше.
- На третьем проходе уже не надо сравнивать предпоследний и третий элемент с конца. Поэтому число сравнений будет на два меньше, чем при первом проходе.
- В конце концов, при проходе по массиву, когда остаются только два элемента, которые надо сравнить, выполняется только одно сравнение.
- После этого первый элемент не с чем сравнивать, и, следовательно, последний проход по массиву не нужен. Другими словами, количество проходов по массиву равно n-1, где n – это количество элементов массива.
- Количество сравнений в каждом проходе равно n-j, где j – это номер прохода по массиву (первый, второй, третий и т.д.).
- При обмене элементов массива обычно используется «буферная» (третья) переменная, куда временно помещается значение одного из элементов.
Delphi/Pascal
const
n = 10; { количество элементов в массиве }
var
a:array of integer;
i,j,buf:integer;
begin
{Заполняем массив случайными целыми числами от 0 до 50 и выводим массив на экран}
for i:=1 to n do
begin
a:=random(50);
write(a:3);
end;
{ сортировка массива по возрастанию }
for j:=1 to n-1 do
for i:= 1 to n-j do {проверяем все элементы до предпоследнего неотсортированного}
if a>a then { ищем элементы, которые стоят неправильно }
begin { меняем элементы местами }
buf:=a;
a:=a;
a:=buf;
end;
writeln;
writeln(‘Массив после сортировки: ‘);
for i:=1 to n do write(a,’ ‘);
end.
|
1 |
const n=10;{количествоэлементоввмассиве} var aarray1..nofinteger; i,j,bufinteger; begin {Заполняеммассивслучайнымицелымичисламиотдо50ивыводиммассивнаэкран} fori:=1tondo begin ai=random(50); write(ai3); end; {сортировкамассиваповозрастанию} forj:=1ton-1do fori=1ton-jdo{проверяемвсеэлементыдопредпоследнегонеотсортированного} ifai>ai+1then{ищемэлементы,которыестоятнеправильно} begin{меняемэлементыместами} buf:=ai; ai=ai+1; ai+1=buf; end; writeln; writeln(‘Массив после сортировки: ‘); fori:=1tondowrite(ai,’ ‘); end. |
Количество просмотров: 4 653
| Категория: Pascal | Тэги: сортировка
Использовать
Пузырьковая сортировка — алгоритм сортировки, который непрерывно просматривает список, меняя местами элементы, пока они не появятся в правильном порядке. Список был построен в декартовой системе координат, где каждая точка ( x , y ) указывает, что значение y хранится в индексе x . Затем список будет отсортирован пузырьковой сортировкой по значению каждого пикселя
Обратите внимание, что сначала сортируется самый большой конец, а меньшим элементам требуется больше времени, чтобы переместиться в правильное положение
Хотя пузырьковая сортировка является одним из простейших алгоритмов сортировки для понимания и реализации, ее сложность O ( n 2 ) означает, что ее эффективность резко снижается в списках из более чем небольшого числа элементов. Даже среди простых алгоритмов сортировки O ( n 2 ) такие алгоритмы, как сортировка вставкой , обычно значительно более эффективны.
Из-за своей простоты пузырьковая сортировка часто используется для ознакомления с концепцией алгоритма или алгоритма сортировки для начинающих студентов- информатиков . Тем не менее, некоторые исследователи, такие как Оуэн Астрахан , пошли на многое, чтобы осудить пузырьковую сортировку и ее неизменную популярность в образовании по информатике, рекомендуя даже не преподавать ее.
Жаргон Файл , который лихо звонков bogosort «архетипический извращенно ужасный алгоритм», также вызывает пузырьковую сортировку «общий плохой алгоритм». Дональд Кнут в своей книге «Искусство компьютерного программирования» пришел к выводу, что «пузырьковая сортировка, кажется, не имеет ничего, что могло бы ее рекомендовать, кроме броского названия и того факта, что она приводит к некоторым интересным теоретическим проблемам», некоторые из которых он затем обсуждает.
Пузырьковая сортировка асимптотически эквивалентна по времени работы сортировке вставкой в худшем случае, но эти два алгоритма сильно различаются по количеству необходимых перестановок. Экспериментальные результаты, такие как результаты Astrachan, также показали, что сортировка вставкой работает значительно лучше даже в случайных списках. По этим причинам многие современные учебники алгоритмов избегают использования алгоритма пузырьковой сортировки в пользу сортировки вставкой.
Пузырьковая сортировка также плохо взаимодействует с современным оборудованием ЦП. Он производит как минимум вдвое больше записей, чем сортировка вставкой, вдвое больше промахов в кеш и асимптотически больше ошибочных прогнозов переходов . Эксперименты с сортировкой строк Astrachan в Java показывают, что пузырьковая сортировка примерно в пять раз быстрее сортировки вставкой и на 70% быстрее сортировки по выбору .
В компьютерной графике пузырьковая сортировка популярна благодаря своей способности обнаруживать очень маленькую ошибку (например, замену всего двух элементов) в почти отсортированных массивах и исправлять ее с линейной сложностью (2 n ). Например, он используется в алгоритме заполнения многоугольника, где ограничивающие линии сортируются по их координате x в определенной строке сканирования (линия, параллельная оси x ), а с увеличением y их порядок изменяется (два элемента меняются местами) только при пересечения двух линий. Пузырьковая сортировка — это стабильный алгоритм сортировки, как и сортировка вставкой.
Использование параметра cmp
Все версии Python 2.x поддерживали параметр для обработки пользовательских функций сравнения. В Python 3.0 от этого параметра полностью избавились. В Python 2.x в можно было передать функцию, которая использовалась бы для сравнения элементов. Она должна принимать два аргумента и возвращать отрицательное значение для случая «меньше чем», положительное — для «больше чем» и ноль, если они равны:
Можно сравнивать в обратном порядке:
При портировании кода с версии 2.x на 3.x может возникнуть ситуация, когда нужно преобразовать пользовательскую функцию для сравнения в функцию-ключ. Следующая обёртка упрощает эту задачу:
Чтобы произвести преобразование, оберните старую функцию:
В Python 2.7 функция была добавлена в модуль functools.
8
Code
function bubbleSort(array a)
for i in 1 -> a.length - 1 do
for j in 1 -> a.length - i - 1 do
if a < a
swap(a, a);
/**
* Bubble sort (descending order)
* @param array array to besorted
*/
public static void bubbleSort(int[] array){
for (int i = 0; i < array.length - 1; i++) {
for (int j = 0; j < array.length - i - 1; j++) {
if(array < array){
int tmp = array;
array = array;
array = tmp;
}
}
}
}
/** * Bubble sort (ascending order) * @param array array to be sorted * @param size size of the array */ void bubbleSort(int * array, int size){ for(int i = 0; i
/**
* Bubble sort (ascending order)
* @param arr array to be sorted
* @author Thomas (www.adamjak.net)
*/
static void BubbleSort(int[] arr)
{
for (int i = 0; i
/**
* Bubble sort (descending order)
* @param array array to be sorted
* @auhor Pavel Micka
*/
function bubbleSort(array){
for (var i = 0; i
procedure BubbleSort(var X : ArrayType; N : integer);
var
I,
J : integer;
begin
for I := 2 to N do
begin
for J := N downto I do
if (X > X) then
Swap(X, X);
end
end;
procedure Swap(var X, Y : integer);
var
Temp : integer;
begin
Temp := X;
X := Y;
Y := Temp
end;
/**
* Bubble sort (ascending order)
* @param arr array to be sorted
* @auhor Thomas (www.adamjak.net)
*/
function bubble_sort(&$arr) {
$count = count($arr);
for($i = 0; $i
Пример сортировки пузыря
Учитывая последовательность: 12, 16, 11, 10, 14, 13 Количество элементов ( n ): 6 Давайте начнем-
Шаг 1: Переменные Я и J Представление отсортированных элементов и позиции.
Шаг 2: N 6. N.
Шаг 3: Установить Я Как 0. я
Шаг 4: Установить J Как 1. j
Шаг 5: Сравнение позиций J и J + 1 Элемент в положении 1 (12) не превышает один при 2 (16).
Шаг 6: Увеличение J Отказ j
Шаг 7: J (2) не N-I (6), поэтому мы идем к шагу 5.
Шаг 5: Положение 2 (16) больше, чем позиция 3 (11), поэтому мы поменяем.
Последовательность: 12, 11 , 16 , 10, 14, 13
Шаг 6: Увеличение J Отказ j
Шаг 7: 3 не 6, поэтому мы идем к шагу 5.
Шаг 5: 16 больше 10, поэтому мы поменяем. Последовательность: 12, 11, 10 , 16 , 14, 13
Шаг 6: Увеличение J Отказ j
Шаг 7: 4 не 6, поэтому мы идем к шагу 5.
Шаг 5: 16 больше 14, поэтому мы поменяем. Последовательность: 12, 11, 10, 14 , 16 13.
Шаг 6: Увеличение J Отказ j
Шаг 7: 5 не 6, поэтому мы идем к шагу 5.
Шаг 5: 16 больше 13, поэтому мы поменяем. Последовательность: 12, 11, 10, 14, 13 , 16.
Шаг 6: Увеличение J Отказ j
Шаг 7: J (6) равен N-I (6), поэтому мы переходим к шагу 8
Обратите внимание, что наибольший элемент (16) находится в конце, и мы отсортировали один элемент наверняка. Шаг 8: Увеличение я
я
Шаг 9: Я (1) не N-1 (5), поэтому мы повторяем все это по сравнению с шагом 4, а цикл продолжается, полученные изменения в последовательности будут выглядеть так:
11 , 12 , 10, 14, 13, 16 11, 10 , 12 , 14, 13, 16 11, 10, 12 , 14 , 13, 16 11, 10, 12, 13 , 14 , 16 10 , 11 12, 13, 14 , 16 10, 11 , 12 , 13, 14 , 16 10, 11, 12 , 13 , 14 , 16 10 , 11 12, 13 , 14 , 16 10, 11 , 12 , 13 , 14 , 16 10 , 11 , 12 , 13 , 14 , 16 10 , 11 , 12 , 13 , 14 , 16.
После этого Я становится 5, что это N-1 Таким образом, контурные контуры и алгоритм говорит нам, что список отсортирован. Также кажется, что список может быть отсортирован до окончания алгоритма, что просто означает, что заданная последовательность была несколько отсортирована до того, как она была передана алгоритму.
Working of Bubble Sort
Suppose we are trying to sort the elements in ascending order.
1. First Iteration (Compare and Swap)
- Starting from the first index, compare the first and the second elements.
- If the first element is greater than the second element, they are swapped.
- Now, compare the second and the third elements. Swap them if they are not in order.
- The above process goes on until the last element.
Compare the Adjacent Elements
2. Remaining Iteration
The same process goes on for the remaining iterations.
After each iteration, the largest element among the unsorted elements is placed at the end.
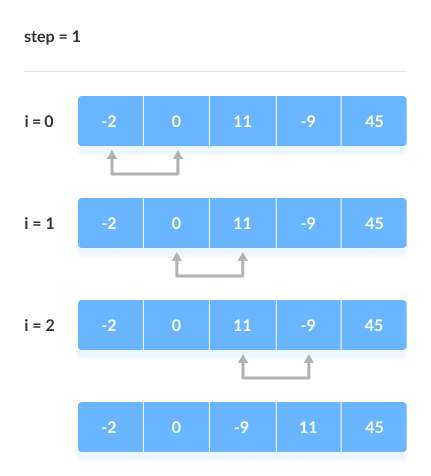Put the largest element at the end
In each iteration, the comparison takes place up to the last unsorted element.
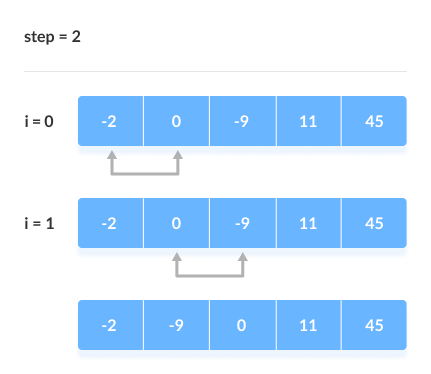Compare the adjacent elements
The array is sorted when all the unsorted elements are placed at their correct positions.
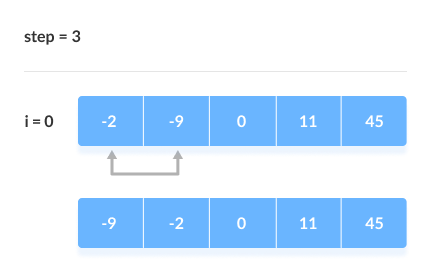The array is sorted if all elements are kept in the right order
Сортировка пузырьком
Идея алгоритма очень простая. Идём по массиву чисел и проверяем порядок (следующее число должно быть больше и равно предыдущему), как только наткнулись на нарушение порядка, тут же обмениваем местами элементы, доходим до конца массива, после чего начинаем сначала.
Отсортируем массив {1, 5, 2, 7, 6, 3}
Идём по массиву, проверяем первое число и второе, они идут в порядке возрастания. Далее идёт нарушение порядка, меняем местами эти элементы
Продолжаем идти по массиву, 7 больше 5, а вот 6 меньше, так что обмениваем из местами
3 нарушает порядок, меняем местами с 7
Возвращаемся к началу массива и проделываем то же самое
void bubbleSort(int *a, size_t size) {
size_t i, j;
int tmp;
for (i = 1; i < size; i++) {
for (j = 1; j < size; j++) {
if (a > a) {
tmp = a;
a = a;
a = tmp;
}
}
}
}
Этот алгоритм всегда будет делать (n-1)2 шагов, независимо от входных данных. Даже если массив отсортирован, всё равно он будет пройден (n-1)2 раз. Более того, будут в очередной раз проверены уже отсортированные данные.
Пусть нужно отсортировать массив 1, 2, 4, 3
После того, как были поменяны местами элемента a и a нет больше необходимости проходить этот участок массива
Примем это во внимание и переделаем алгоритм
void bubbleSort2(int *a, size_t size) {
size_t i, j;
int tmp;
for (i = 1; i < size; i++) {
for (j = i; j > 0; j--) {
if (a < a) {
tmp = a;
a = a;
a = tmp;
}
}
}
}
Ещё одна реализация
void bubbleSort2b(int *a, size_t size) {
size_t i, j;
int tmp;
for (i = 1; i < size; i++) {
for (j = 1; j <= size-i; j++) {
if (a < a) {
tmp = a;
a = a;
a = tmp;
}
}
}
}
В данном случае будет уже вполовину меньше шагов, но всё равно остаётся проблема сортировки уже отсортированного массива: нужно сделать так, чтобы отсортированный массив функция просматривала один раз. Для этого введём переменную-флаг: он будет опущен (flag = 0), если массив отсортирован. Как только мы наткнёмся на нарушение порядка, то флаг будет поднят (flag = 1) и мы начнём сортировать массив как обычно.
void bubbleSort3(int *a, size_t size) {
size_t i;
int tmp;
char flag;
do {
flag = 0;
for (i = 1; i < size; i++) {
if (a < a) {
tmp = a;
a = a;
a = tmp;
flag = 1;
}
}
} while (flag);
}
В этом случае сложность также порядка n2, но в случае отсортированного массива будет всего один проход.
Теперь усовершенствуем алгоритм. Напишем функцию общего вида, чтобы она сортировала массив типа void. Так как тип переменной не известен, то нужно будет дополнительно передавать размер одного элемента массива и функцию сравнения.
int intSort(const void *a, const void *b) {
return *((int*)a) > *((int*)b);
}
void bubbleSort3g(void *a, size_t item, size_t size, int (*cmp)(const void*, const void*)) {
size_t i;
void *tmp = NULL;
char flag;
tmp = malloc(item);
do {
flag = 0;
for (i = 1; i < size; i++) {
if (cmp(((char*)a + i*item), ((char*)a + (i-1)*item))) {
memcpy(tmp, ((char*)a + i*item), item);
memcpy(((char*)a + i*item), ((char*)a + (i-1)*item), item);
memcpy(((char*)a + (i-1)*item), tmp, item);
flag = 1;
}
}
} while (flag);
free(tmp);
}
Функция выглядит некрасиво – часто вычисляется адрес текущего и предыдущего элемента. Выделим отдельные переменные для этого.
void bubbleSort3gi(void *a, size_t item, size_t size, int (*cmp)(const void*, const void*)) {
size_t i;
void *tmp = NULL;
void *prev, *cur;
char flag;
tmp = malloc(item);
do {
flag = 0;
i = 1;
prev = (char*)a;
cur = (char*)prev + item;
while (i < size) {
if (cmp(cur, prev)) {
memcpy(tmp, prev, item);
memcpy(prev, cur, item);
memcpy(cur, tmp, item);
flag = 1;
}
i++;
prev = (char*)prev + item;
cur = (char*)cur + item;
}
} while (flag);
free(tmp);
}
Теперь с помощью этих функций можно сортировать массивы любого типа, например
void main() {
int a = {1, 0, 9, 8, 7, 6, 2, 3, 4, 5};
int i;
bubbleSort3gi(a, sizeof(int), 10, intSort);
for (i = 0; i < 10; i++) {
printf("%d ", a);
}
_getch();
}
Быстрая сортировка
Этот алгоритм также относится к алгоритмам «разделяй и властвуй». Его используют чаще других алгоритмов, описанных в этой статье. При правильной конфигурации он чрезвычайно эффективен и не требует дополнительной памяти, в отличие от сортировки слиянием. Массив разделяется на две части по разные стороны от опорного элемента. В процессе сортировки элементы меньше опорного помещаются перед ним, а равные или большие —позади.
Алгоритм
Быстрая сортировка начинается с разбиения списка и выбора одного из элементов в качестве опорного. А всё остальное передвигаем так, чтобы этот элемент встал на своё место. Все элементы меньше него перемещаются влево, а равные и большие элементы перемещаются вправо.
Реализация
Существует много вариаций данного метода. Способ разбиения массива, рассмотренный здесь, соответствует схеме Хоара (создателя данного алгоритма).
Время выполнения
В среднем время выполнения быстрой сортировки составляет O(n log n).
Обратите внимание, что алгоритм быстрой сортировки будет работать медленно, если опорный элемент равен наименьшему или наибольшему элементам списка. При таких условиях, в отличие от сортировок кучей и слиянием, обе из которых имеют в худшем случае время сортировки O(n log n), быстрая сортировка в худшем случае будет выполняться O(n²)
What is Sorting — Definition
Often in real life, we are supposed to arrange data in a particular order. For instance, during our school days, we are told to stand in the queue based on our heights. Another example is the attendance register at school/college which contains our names arranged in alphabetical order.
These data arrangements give easier access to data for future use for ex. finding «Joe» in an attendance register of 100 students. The arrangement of data in a particular order is called as sorting of the data by that order. 2 of the most commonly used orders are:
- Ascending order: while sorting the data in ascending order, we try to arrange the data in a way such that each element is in some way “smaller than” its successor. This “smaller than” relation is an ordered relation over the set from which the data is taken. As a simple example, the numbers 1, 2, 3, 4, 5 are sorted in ascending order. Here, the “smaller than” relation is actually the “<” operator. As can be seen, 1 < 2 < 3 < 4 < 5.
- Descending order: descending order is the exact opposite of ascending order. Given a data that is sorted in ascending order, reverse it and you will get the data in descending order.
Due to the similar nature of the 2 orders, we often drop the actual order and we say — we want to sort the data. This generally means that we want the data to be sorted in ascending order. Before we get into the details of the sorting algorithm, let us understand the problem statement.
Сортировка слиянием
Этот алгоритм относится к алгоритмам «разделяй и властвуй». Он разбивает список на две части, каждую из них он разбивает ещё на две и т. д. Список разбивается пополам, пока не останутся единичные элементы.
Соседние элементы становятся отсортированными парами. Затем эти пары объединяются и сортируются с другими парами. Этот процесс продолжается до тех пор, пока не отсортируются все элементы.
Алгоритм
Список рекурсивно разделяется пополам, пока в итоге не получатся списки размером в один элемент. Массив из одного элемента считается упорядоченным. Соседние элементы сравниваются и соединяются вместе. Это происходит до тех пор, пока не получится полный отсортированный список.
Сортировка осуществляется путём сравнения наименьших элементов каждого подмассива. Первые элементы каждого подмассива сравниваются первыми. Наименьший элемент перемещается в результирующий массив. Счётчики результирующего массива и подмассива, откуда был взят элемент, увеличиваются на 1.
Реализация
Обратите внимание, что функция , в отличие от предыдущих алгоритмов, возвращает новый список, а не сортирует существующий. Поэтому такая сортировка требует больше памяти для создания нового списка того же размера, что и входной список
Декорируем-сортируем-раздекорируем
- Сначала исходный список пополняется новыми значениями, контролирующими порядок сортировки.
- Затем новый список сортируется.
- После этого добавленные значения убираются, и в итоге остаётся отсортированный список, содержащий только исходные элементы.
Вот так можно отсортировать данные учеников по оценке:
Это работает из-за того, что кортежи сравниваются лексикографически, сравниваются первые элементы, а если они совпадают, то сравниваются вторые и так далее.
Не всегда обязательно включать индекс в декорируемый список, но у него есть преимущества:
- Сортировка стабильна — если у двух элементов одинаковый ключ, то их порядок не изменится.
- У исходных элементов не обязательно должна быть возможность сравнения, так как порядок декорированных кортежей будет определяться максимум по первым двум элементам. Например, исходный список может содержать комплексные числа, которые нельзя сравнивать напрямую.
Ещё эта идиома называется преобразованием Шварца в честь Рэндела Шварца, который популяризировал её среди Perl-программистов.
Для больших списков и версий Python ниже 2.4, «декорируем-сортируем-раздекорируем» будет оптимальным способом сортировки. Для версий 2.4+ ту же функциональность предоставляют функции-ключи.
7
Сортировка пузырьком
Этот метод, вероятно, является первым достаточно сложным модулем, который должен написать любой начинающий программист. Это очень простая конструкция, которая знакомит учащихся с основами работы алгоритмов.
Пузырьковая (обменная) использует двумерный или одномерный массив и механизм обмена. Большинство языков программирования имеют встроенную функцию для перестановки элементов. Даже если функция обмена не существует, требуется всего пара дополнительных строк кода. Вместо перебора массива, пузырьковая работает по схеме сравнения соседних пар объектов. Шаги:
- Если элементы расположены не в правильном порядке, они меняются местами так, что самый большой из двух перемещается вверх. Этот процесс продолжается до тех пор, пока самый большой из объектов, не окажется на первом месте.
- После этого начинается поиск следующего по величине элемента.
- Перестановка остановится, когда весь массив окажется в правильном порядке.
Сортировка пузырьком на Pascal (Паскаль):
Сортировка массива методом пузырька на Python (Питон):
На Java:
Из-за своей простоты этот метод часто используется для представления концепции алгоритма сортировки. В компьютерной графике она популярна благодаря своей способности выявлять очень маленькую ошибку (например, перестановку всего двух элементов) в почти отсортированных массивах и исправлять ее с помощью линейной сложности.
Какой способ обработки данных выбрать, специалист решает сам, в зависимости от времени и объема информации.
Difference between Selection, Bubble and Insertion Sort
-
In terms of algorithm
- In Bubble sort, adjacent elements are compared and sorted if they are in the wrong order.
- In Selection Sort, we select the smallest element and swap it with the 0th index element in the first iteration. This selection continues for n-1 elements and the single element is already sorted and we will have array sorted by 1 element in every iteration
- In Insertion sort, we create partitions of sorted and unsorted parts. One by one element from the sorted art is taken and sent to the unsorted part for checking and placing it to the right position in sorting using swaps.
-
In terms of time and space complexity
- All 3 sort have O(n2) time complexity. But via flag variable we can reduce the time complexity of bubble and insertion to O(n) is the best case.
- Space Complexity is the same for all i.e., O(1)
| Best | Average | Worst | Space | |
| Selection | O(n2) | O(n2) | O(n2) | O(1) |
| Bubble | O(n) | O(n2) | O(n2) | O(1) |
| Insertion | O(n) | O(n2) | O(n2) | O(1) |
-
In terms of speed
- Bubble sort is slower than the maximum sort algorithm.
- There are a lot of swaps that might take place in the worst case.
-
In terms of in-place
- In-place states that the algorithm is in-place if it does not need extra memory barring some variable creation which counts to constant space.
- Selection, Bubble and Insertion are in-place algorithms and do not require any auxiliary memory.
-
In terms of stability
- Stability states that the algorithm is stable if the relative ordering of the same elements in the input and output array remains the same.
- Bubble and Insertion are stable algorithms but the naive selection is not as swapping may cost stability.
| Selection | Bubble | Insertion |
| Select smallest in every iteration do single swap | An adjacent swap of every element with the other element where ordering is incorrect | Take and put the element one by one and put it in the right place in the sorted part. |
| Best case time complexity is O(n2) | Best case time complexity is O(n) | Best case time complexity is O(n) |
| Works better than bubble as no of swaps are significantly low | Worst efficiency as too many swaps are required in comparison to selection and insertion | Works better than bubble as no of swaps are significantly low |
| It is in-place | It is in-place | It is in-place |
| Not stable | Stable | Stable |
This brings us to the end of this article where we learned about bubble sort and its implementation in different languages. Also, we learned how to optimize this algorithm to get better performance. I would highly suggest to take up this free course for data structures and algorithms to improve your coding skills.
Analysis
There are outer iterations needed to sort the array, because every iteration puts one element to it’s place. Every inner iteration needs one step less the previous one, since the problem size is gradually decreasing.
Last part of the algorithm is a condition, which decides whether we should swap the adjacent elements.
Complexity
The complexity of the condition (and possible swap) is obviously constant (). The inner cycle will be performed
times.
Which is in total (according to the formula for arithmetic sequence):
Because this number represents the best and the worst case of algorithm behavior, it’s asymptotic complexity after omitting additive and multiplicative constants is .
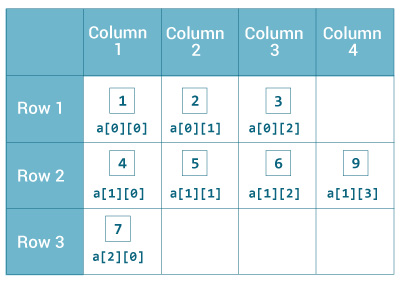
Сортировка многомерного массива
Сортировка статического многомерного массива по существу не отличается от сортировки одномерного. Можно воспользоваться тем свойством, что статический одномерный и многомерный массивы имеют одинаковое представление в памяти.
void main() {
int a = {1, 9, 2, 8, 3, 7, 4, 6, 5};
int i, j;
bubbleSort3gi(a, sizeof(int), 9, intSort);
for (i = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
printf("%d ", a);
}
}
}
#include <conio.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void bubbleSort2d(int **a, size_t m, size_t n) {
int tmp;
size_t i, j, k, jp, ip;
size_t size = m*n;
char flag;
do {
flag = 0;
for (k = 1; k < size; k++) {
//Вычисляем индексы текущего элемента
j = k / m;
i = k - j*m;
//Вычисляем индексы предыдущего элемента
jp = (k-1) / m;
ip = (k-1) - jp*m;
if (a > a) {
tmp = a;
a = a;
a = tmp;
flag = 1;
}
}
} while(flag);
}
#define SIZE_X 3
#define SIZE_Y 4
void main() {
int **a = NULL;
int i, j;
a = (int**) malloc(sizeof(int*) * SIZE_X);
for (i = 0; i < SIZE_X; i++) {
a = (int*) malloc(sizeof(int) * SIZE_Y);
for (j = 0; j < SIZE_Y; j++) {
a = rand();
printf("%8d ", a);
}
printf("\n");
}
printf("\nafter sort\n");
bubbleSort2d(a, SIZE_X, SIZE_Y);
for (i = 0; i < SIZE_X; i++) {
for (j = 0; j < SIZE_Y; j++) {
printf("%8d ", a);
}
printf("\n");
}
for (i = 0; i < SIZE_X; i++) {
free(a);
}
free(a);
_getch();
}
Во-вторых, можно сначала переместить массив в одномерный, отсортировать одномерный массив, после чего переместить его обратно в двумерный.
void bubbleSort3gi2d(void **a, size_t item, size_t m, size_t n, int (*cmp)(const void*, const void*)) {
size_t size = m*n, sub_size = n*item;
size_t i, j, k;
void *arr = malloc(size * item);
char *p1d = (char*)arr;
char *p2d = (char*)a;
//Копируем двумерный массив типа void в одномерный
for (i = 0; i < m; i++) {
memcpy(p1d + i*sub_size, *((void**)(p2d + i*item)), sub_size);
}
bubbleSort3gi(arr, item, size, cmp);
//Копируем одномерный массив обратно в двумерный
for (i = 0; i < m; i++) {
memcpy(*((void**)(p2d + i*item)), p1d + i*sub_size, sub_size);
}
}
Если вас смущает эта функция, то воспользуйтесь типизированной. Вызов, из предыдущего примера
bubbleSort3gi2d((void**)a, sizeof(int), SIZE_X, SIZE_Y, intSort);
Q&A
Всё ещё не понятно? – пиши вопросы на ящик
Подробный разбор пузырьковой сортировки
Давайте разберем подробно как работает пузырьковая сортировка
Первая итереация (первый повтор алгоритма) меняет между собой 4 и 2 так как цифра два меньше чем четыре 2<4, повторюсь что алгоритм меняет значения между собой если, слева оно меньше чем справа. Далее происходит сверка между 4 и 3, и так как 3 меньше чем 4 (3<4) происходит обмен значениями. Потом проходит проверку между 4 и 8 и так как значение 4 меньше чем 8 то не происходит обмена, ведь уже и так всё на своих местах.
Далее сравнивается 8 и 1 и так как 1 меньше чем 8 (1<8) и оно не находиться слева то происходит обмен значениями.После это первый повтор алгоритма заканчивается, на анимации я выделил это зеленым фоном.
В итоге по окончанию работы алгоритма пузырьковой сортировки мы имеем следующий порядок числового массива: 2 3 4 1 8
и начинается второй повтор алгоритма.
Далее сравнивается 2 и 3 и так как два меньше чем три и оно находиться слева то просто идем дальше ничего не трогая. Также проверяем и 3 и 4 и тоже самое условие выполняется 3<4 и оно слева. Дальше проверяется 4 и 1 и тут мы видим что число 1<4 и не находиться слева, поэтому алгоритм меняет их местами. В крайний раз для второго повторения алгоритма проверяется 4 и 8, но тут всё в порядке, и мы дошли до конца начинаем третье повторение. Итоги для второго повторения такие : 2 3 1 4 8
Третье повторение пузырькового алгоритма начинается с сравнения 2 и 3, тут алгоритм проверяет что 2<3 и 2 находиться слева и оставляет их в покое и идет дальше. Сравнение же 3 и 1 показывает что 1 то меньше чем три, но почему то не слева и меняет их местами. Далее идет сравнение 3 и 4, тут всё в порядке и так далее до сравнения 4 и 8.
После этого получается следующий результат: 2 1 3 4 8
Как мы видим почти все цифры уже на своих местах и в порядке возрастания! Осталось только в последнем повторении пузырькового алгоритма поменять местами 2 и 1 и всё. После того как алгоритм закончил свою работу и проверил что цифры больше нельзя поменять местами он перестает работать с таким вот результатом: 1 2 3 4 8
