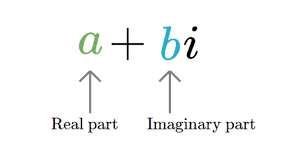Десятичный модуль(decimal) python

Содержание:

Преобразование числовых типов
Гиперболические функции
Игра в кости с использованием модуля random в Python
Графический интерфейс
Практическая работа. Создание собственного модуля
Тригонометрические функции в Python
Классификационные функции
Фаза комплексного числа
Математические методы
Игра в кости с использованием модуля random в Python
Функция экспоненты exp() в Python
Вычисление квадратного корня в Python с помощью модуля cmath
Комбинации элементов между собой
Фаза (аргумент) сложного числа
Звук
Тригонометрические функции
Заключение

Преобразование числовых типов

В Python есть два : (integer) и числа с (float).

Бывает, вы работаете над чужим кодом и вам нужно преобразовать целое число в число с плавающей запятой (и наоборот). Или вы можете обнаружить, что использовали целое число, хотя на самом деле вам нужно число с плавающей запятой. Python имеет встроенные методы, позволяющие легко выполнить все эти преобразования.

Преобразование целых чисел в числа с плавающей запятой

Метод Python преобразует целые числа в числа с плавающей запятой. Чтобы использовать эту функцию, добавьте в скобки целое число:

float(57)

В этом случае 57 будет преобразовано в 57.0.

Этот метод можно использовать и с переменной. Объявим равным 57, а затем выведем новое значение с плавающей запятой:

f = 57
print(float(f))

Результат:

Используя функцию , мы можем преобразовывать целые числа в числа с плавающей запятой.

Преобразование чисел с плавающей запятой в целые числа

Python также имеет встроенную функцию для преобразования чисел с плавающей запятой в целые числа: .

Функция работает аналогично функции . Чтобы преобразовать десятичную дробь в целое число, вы можете добавить его внутрь скобок:

int(390.8)

В этом случае 390.8 будет преобразовано в 390.

Эту функцию можно использовать и с переменными. Давайте объявим равным 125.0, а — равным 390.8, а затем применим к переменным функцию :

b = 125.0
c = 390.8

print(int(b))
print(int(c))

Результат:

При преобразовании чисел с плавающей запятой в целые числа с помощью функции Python отсекает все, что идет после запятой. Мы можем ожидать, что 390,8 округлится до 391, но с применением только лишь функции этого не произойдет.

Преобразование чисел путем деления

В Python 3 при делении одного целого числа на другое целое число результат преобразуется в число с плавающей запятой. То есть, если разделить 5 на 2, в Python 3 вы получите число с плавающей запятой:

a = 5 / 2
print(a)

В Python 2, так как вы имели дело с двумя целыми числами, вы получите ответ в виде целого числа: 5 / 2 = 2. Прочтите «Python 2 vs Python 3: Практические соображения» для получения дополнительной информации о различиях между Python 2 и Python 3.

Гиперболические функции

Генерация случайных чисел

c = 2 + 2j
print('inverse hyperbolic sine =', cmath.asinh(c))
print('inverse hyperbolic cosine =', cmath.acosh(c))
print('inverse hyperbolic tangent =', cmath.atanh(c))

print('hyperbolic sine =', cmath.sinh(c))
print('hyperbolic cosine =', cmath.cosh(c))
print('hyperbolic tangent =', cmath.tanh(c))

Вывод:

inverse hyperbolic sine = (1.7343245214879666+0.7542491446980459j)
inverse hyperbolic cosine = (1.7343245214879666+0.8165471820968505j)
inverse hyperbolic tangent = (0.2388778612568591+1.311223269671635j)
hyperbolic sine = (-1.5093064853236156+3.4209548611170133j)
hyperbolic cosine = (-1.5656258353157435+3.2978948363112366j)
hyperbolic tangent = (1.0238355945704727-0.028392952868232294j)

Игра в кости с использованием модуля random в Python

Псевдослучайные числа

Далее представлен код простой игры в кости, которая поможет понять принцип работы функций модуля random. В игре два участника и два кубика.

Участники по очереди бросают кубики, предварительно встряхнув их;
Алгоритм высчитывает сумму значений кубиков каждого участника и добавляет полученный результат на доску с результатами;
Участник, у которого в результате большее количество очков, выигрывает.

Код программы для игры в кости Python:

Python

import random

PlayerOne = «Анна»
PlayerTwo = «Алекс»

AnnaScore = 0
AlexScore = 0

# У каждого кубика шесть возможных значений
diceOne =
diceTwo =

def playDiceGame():
«»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»»

for i in range(5):
#оба кубика встряхиваются 5 раз
random.shuffle(diceOne)
random.shuffle(diceTwo)
firstNumber = random.choice(diceOne) # использование метода choice для выбора случайного значения
SecondNumber = random.choice(diceTwo)
return firstNumber + SecondNumber

print(«Игра в кости использует модуль random\n»)

#Давайте сыграем в кости три раза
for i in range(3):
# определим, кто будет бросать кости первым
AlexTossNumber = random.randint(1, 100) # генерация случайного числа от 1 до 100, включая 100
AnnaTossNumber = random.randrange(1, 101, 1) # генерация случайного числа от 1 до 100, не включая 101

if( AlexTossNumber > AnnaTossNumber):
print(«Алекс выиграл жеребьевку.»)
AlexScore = playDiceGame()
AnnaScore = playDiceGame()
else:
print(«Анна выиграла жеребьевку.»)
AnnaScore = playDiceGame()
AlexScore = playDiceGame()

if(AlexScore > AnnaScore):
print («Алекс выиграл игру в кости. Финальный счет Алекса:», AlexScore, «Финальный счет Анны:», AnnaScore, «\n»)
else:
print(«Анна выиграла игру в кости. Финальный счет Анны:», AnnaScore, «Финальный счет Алекса:», AlexScore, «\n»)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

importrandom

PlayerOne=»Анна»

PlayerTwo=»Алекс»

AnnaScore=

AlexScore=

# У каждого кубика шесть возможных значений

diceOne=1,2,3,4,5,6

diceTwo=1,2,3,4,5,6

defplayDiceGame()

«»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»»

foriinrange(5)

#оба кубика встряхиваются 5 раз

random.shuffle(diceOne)

random.shuffle(diceTwo)

firstNumber=random.choice(diceOne)# использование метода choice для выбора случайного значения

SecondNumber=random.choice(diceTwo)

returnfirstNumber+SecondNumber

print(«Игра в кости использует модуль random\n»)

#Давайте сыграем в кости три раза

foriinrange(3)

# определим, кто будет бросать кости первым

AlexTossNumber=random.randint(1,100)# генерация случайного числа от 1 до 100, включая 100

AnnaTossNumber=random.randrange(1,101,1)# генерация случайного числа от 1 до 100, не включая 101

if(AlexTossNumber>AnnaTossNumber)

print(«Алекс выиграл жеребьевку.»)

AlexScore=playDiceGame()

AnnaScore=playDiceGame()

else

print(«Анна выиграла жеребьевку.»)

AnnaScore=playDiceGame()

AlexScore=playDiceGame()

if(AlexScore>AnnaScore)

print(«Алекс выиграл игру в кости. Финальный счет Алекса:»,AlexScore,»Финальный счет Анны:»,AnnaScore,»\n»)

else

print(«Анна выиграла игру в кости. Финальный счет Анны:»,AnnaScore,»Финальный счет Алекса:»,AlexScore,»\n»)

Вывод:

Shell

Игра в кости использует модуль random

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 5 Финальный счет Алекса: 2

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 2

Алекс выиграл жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 8

1
2
3
4
5
6
7
8
9
10

Игравкостииспользуетмодульrandom

Аннавыигралажеребьевку.

Аннавыигралаигрувкости.ФинальныйсчетАнны5ФинальныйсчетАлекса2

Аннавыигралажеребьевку.

Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса2

Алексвыигралжеребьевку.

Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса8

Вот и все. Оставить комментарии можете в секции ниже.

Графический интерфейс

Math.random()

В стандартной библиотеке Python есть
графическая библиотека интерфейсов
Tkinter. Но при помощи внешних модулей вы
можете поднять GUI ваших приложений на
новый уровень.

wxPython. Создает по-настоящему нативные пользовательские интерфейсы для Python-приложений, которые могут запускаться на Windows, Mac и Linux, а также прочих Unix-подобных системах практически без каких-либо модификаций.

PyGObject. Пакет Python, предоставляющий привязки для библиотек на базе Gobject, таких как GTK, GStreamer, WebKitGTK, GLib, GIO и др.

Pmw. Набор инструментов для создания на Python высокоуровневых составных виджетов (с использованием модуля Tkinter).

WCK. Расширение API, позволяющее реализовывать на чистом Python всевозможные пользовательские виджеты.

Tix. Мощный набор компонентов пользовательского интерфейса, при помощи которого можно расширить возможности ваших Tcl/Tk и Python-приложений. Использование Tix вместе с Tk очень улучшает внешний вид и функционал приложений.

Практическая работа. Создание собственного модуля

Программист на Python всегда может создать собственный модуль, чтобы использовать его в нескольких своих программах или даже предоставить в пользование всему миру. В качестве тренировки создадим модуль с функциями для вычисления площадей прямоугольника, треугольника и круга:

from math import pi, pow
 
def rectangle(a, b):
    return round(a * b, 2)
 
def triangle(a, h):
    return round(0.5 * a * h, 2)
 
def circle(r):
    return round(pi * pow(r, 2), 2)

Здесь также иллюстрируется принцип, что один модуль может импортировать другие. В данном случае импортируются функции из модуля .

Поместите данный код в отдельный файл square.py. Однако куда поместить сам файл?

Когда интерпретатор Питона встречает команду импорта, то просматривает на наличие файла-модуля определенные каталоги. Их перечень можно увидеть по содержимому :

>>> import sys
>>> sys.path
['', '/usr/lib/python35.zip', 
'/usr/lib/python3.5', 
'/usr/lib/python3.5/plat-x86_64-linux-gnu',
'/usr/lib/python3.5/lib-dynload', 
'/home/pl/.local/lib/python3.5/site-packages',
'/usr/local/lib/python3.5/dist-packages', 
'/usr/lib/python3/dist-packages']

Это список адресов в Linux. В Windows он будет несколько другим. Первый элемент – пустая строка, что обозначает текущий каталог, то есть то место, где сохранена сама программа, импортирующая модуль. Если вы сохраните файл-модуль и файл-программу в одном каталоге, то интерпретатор без труда найдет модуль.

Также модуль можно положить в любой другой из указанных в списке каталогов. Тогда он будет доступен для всех программ на Python, а также его можно будет импортировать в интерактивном режиме.

Можно добавить в свой каталог. Однако в этом случае либо код программы должен содержать команды изменения значения , либо надо править конфигурационный файл операционной системы. В большинстве случаев лучше так не делать.

Поместите файл square.py в тот же каталог, где будет исполняемая программа. Ее код должен включать инструкцию импорта модуля square (при импорте расширение файла не указывается) и вызов той функции и с теми параметрами, которые ввел пользователь. То есть у пользователя надо спросить, площадь какой фигуры он хочет вычислить. Далее запросить у него аргументы для соответствующей функции. Передать их в функцию из модуля square, а полученный оттуда результат вывести на экран.

Примечание. Исполнение модуля как самостоятельного скрипта, а также создание строк документации, которые отображает встроенная в Python функция , будут рассмотрены в курсе объектно-ориентированного программирования.

Тригонометрические функции в Python

Модуль math в Python поддерживает все тригонометрические функции. Самые популярные представлены ниже:

: Возвращает синус в радианах;
: Возвращает косинус в радианах;
: Возвращает тангенс в радианах;
: Возвращает инвертированный синус. Аналогичным образом работают и ;
: Конвертирует угол из радиан в градусы;
: Конвертирует угол из градусов в радианы.

Рассмотрим следующий пример:

Python

import math

angle_In_Degrees = 62
angle_In_Radians = math.radians(angle_In_Degrees)

print(‘Значение угла:’, angle_In_Radians)
print(‘sin(x) равен:’, math.sin(angle_In_Radians))
print(‘tan(x) равен:’, math.tan(angle_In_Radians))
print(‘cos(x) равен:’, math.cos(angle_In_Radians))

1
2
3
4
5
6
7
8
9

importmath

angle_In_Degrees=62

angle_In_Radians=math.radians(angle_In_Degrees)

print(‘Значение угла:’,angle_In_Radians)

print(‘sin(x) равен:’,math.sin(angle_In_Radians))

print(‘tan(x) равен:’,math.tan(angle_In_Radians))

print(‘cos(x) равен:’,math.cos(angle_In_Radians))

Вывод

Shell

Значение угла: 1.0821041362364843
sin(x) равен: 0.8829475928589269
tan(x) равен: 1.8807264653463318
cos(x) равен: 0.46947156278589086

1
2
3
4

Значениеугла1.0821041362364843

sin(x)равен0.8829475928589269

tan(x)равен1.8807264653463318

cos(x)равен0.46947156278589086

Обратите внимание, что вначале мы конвертировали значение угла из градусов в радианы для осуществления дальнейших операций

Классификационные функции

Есть несколько разных функций, чтобы проверить, является ли комплексное число конечным, бесконечным или нан. Также есть функция проверки близости двух комплексных чисел.

print(cmath.isfinite(2 + 2j))  # True
print(cmath.isfinite(cmath.inf + 2j))  # False

print(cmath.isinf(2 + 2j))  # False
print(cmath.isinf(cmath.inf + 2j))  # True
print(cmath.isinf(cmath.nan + 2j))  # False


print(cmath.isnan(2 + 2j))  # False
print(cmath.isnan(cmath.inf + 2j))  # False
print(cmath.isnan(cmath.nan + 2j))  # True

print(cmath.isclose(2+2j, 2.01+1.9j, rel_tol=0.05))  # True
print(cmath.isclose(2+2j, 2.01+1.9j, abs_tol=0.005))  # False

Фаза комплексного числа

Фаза комплексного числа – это угол между действительной осью и вектором, представляющим мнимую часть. Изображение ниже иллюстрирует фазу комплексного числа и то, как получить это значение с помощью модулей cmath и math.

Обратите внимание, что фаза, возвращаемая модулями math и cmath, выражается в радианах, мы можем использовать функцию numpy.degrees(), чтобы преобразовать ее в градусы. Диапазон фазы – от -π до + π (от -pi до + pi) в радианах, что эквивалентно от -180 до +180 градусов

import cmath, math, numpy

c = 2 + 2j

# phase
phase = cmath.phase(c)
print('2 + 2j Phase =', phase)
print('Phase in Degrees =', numpy.degrees(phase))
print('-2 - 2j Phase =', cmath.phase(-2 - 2j), 'radians. Degrees =', numpy.degrees(cmath.phase(-2 - 2j)))

# we can get phase using math.atan2() function too
print('Complex number phase using math.atan2() =', math.atan2(2, 1))

Вывод:

2 + 2j Phase = 0.7853981633974483
Phase in Degrees = 45.0
-2 - 2j Phase = -2.356194490192345 radians. Degrees = -135.0
Complex number phase using math.atan2() = 1.1071487177940904

Математические методы

Метод	Описание
math.acos()	Возвращает арккосинус числа.
math.acosh()	Возвращает обратный гиперболический косинус числа.
math.asin()	Возвращает арксинус числа.
math.asinh()	Возвращает обратный гиперболический синус числа.
math.atan()	Возвращает арктангенс числа в радианах.
math.atan2()	Возвращает арктангенс y / x в радианах.
math.atanh()	Возвращает обратный гиперболический тангенс числа.
math.ceil()	Округляет число до ближайшего целого.
math.comb()	Возвращает количество способов выбрать k элементов из n элементов без повторения и порядка.
math.copysign()	Возвращает число с плавающей запятой, состоящее из значения первого параметра и знака второго параметра.
math.cos()	Возвращает косинус числа.
math.cosh()	Возвращает гиперболический косинус числа.
math.degrees()	Преобразует угол из радиан в градусы.
math.dist()	Возвращает евклидово расстояние между двумя точками (p и q), где p и q — координаты этой точки
math.erf()	Возвращает функцию ошибки числа.
math.erfc()	Возвращает дополнительную функцию ошибок числа.
math.exp()	Возвращает E в степени x.
math.expm1()	Возврат Ex — 1
math.fabs()	Возвращает абсолютное значение числа.
math.factorial()	Возвращает факториал числа.
math.floor()	Округляет число до ближайшего целого.
math.fmod()	Возвращает остаток от x / y.
math.frexp()	Возвращает мантиссу и показатель степени указанного числа.
math.fsum()	Возвращает сумму всех элементов в любой итерации (кортежи, массивы, списки и т. Д.)
math.gamma()	Возвращает гамма-функцию в точке x.
math.gcd()	Возвращает наибольший общий делитель двух целых чисел.
math.hypot()	Возвращает евклидову норму.
math.isclose()	Проверяет, близки ли два значения друг к другу или нет
math.isfinite()	Проверяет, является ли число конечным или нет
math.isinf()	Проверяет, бесконечно ли число
math.isnan()	Проверяет, является ли значение NaN (не числом) или нет
math.isqrt()	Округляет квадратный корень вниз до ближайшего целого числа.
math.ldexp()	Возвращает значение, обратное math.frexp (). что является x * (2 ** i) заданных чисел x и i
math.lgamma()	Возвращает логарифмическое значение гаммы x.
math.log()	Возвращает натуральный логарифм числа или логарифм числа по основанию.
math.log10()	Возвращает десятичный логарифм числа x.
math.log1p()	Возвращает натуральный логарифм 1 + x.
math.log2()	Возвращает логарифм x по основанию 2.
math.perm()	Возвращает количество способов выбрать k элементов из n элементов с порядком и без повторения.
math.pow()	Возвращает значение x в степени y.
math.prod()	Возвращает произведение всех элементов в итерируемом объекте.
math.radians()	Преобразует значение градуса в радианы
math.remainder()	Возвращает ближайшее значение, при котором числитель полностью делится на знаменатель.
math.sin()	Возвращает синус числа.
math.sinh()	Возвращает гиперболический синус числа.
math.sqrt()	Возвращает квадратный корень числа.
math.tan()	Возвращает тангенс числа.
math.tanh()	Возвращает гиперболический тангенс числа.
math.trunc()	Возвращает усеченные целые части числа.

Игра в кости с использованием модуля random в Python

Участники по очереди бросают кубики, предварительно встряхнув их;
Алгоритм высчитывает сумму значений кубиков каждого участника и добавляет полученный результат на доску с результатами;
Участник, у которого в результате большее количество очков, выигрывает.

Код программы для игры в кости Python:

Python

import random

PlayerOne = «Анна»
PlayerTwo = «Алекс»

AnnaScore = 0
AlexScore = 0

# У каждого кубика шесть возможных значений
diceOne =
diceTwo =

def playDiceGame():
«»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»»

print(«Игра в кости использует модуль random\n»)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

importrandom

PlayerOne=»Анна»

PlayerTwo=»Алекс»

AnnaScore=

AlexScore=

# У каждого кубика шесть возможных значений

diceOne=1,2,3,4,5,6

diceTwo=1,2,3,4,5,6

defplayDiceGame()

«»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»»

foriinrange(5)

#оба кубика встряхиваются 5 раз

random.shuffle(diceOne)

random.shuffle(diceTwo)

firstNumber=random.choice(diceOne)# использование метода choice для выбора случайного значения

SecondNumber=random.choice(diceTwo)

returnfirstNumber+SecondNumber

print(«Игра в кости использует модуль random\n»)

#Давайте сыграем в кости три раза

foriinrange(3)

# определим, кто будет бросать кости первым

AlexTossNumber=random.randint(1,100)# генерация случайного числа от 1 до 100, включая 100

AnnaTossNumber=random.randrange(1,101,1)# генерация случайного числа от 1 до 100, не включая 101

if(AlexTossNumber>AnnaTossNumber)

print(«Алекс выиграл жеребьевку.»)

AlexScore=playDiceGame()

AnnaScore=playDiceGame()

else

print(«Анна выиграла жеребьевку.»)

AnnaScore=playDiceGame()

AlexScore=playDiceGame()

if(AlexScore>AnnaScore)

print(«Алекс выиграл игру в кости. Финальный счет Алекса:»,AlexScore,»Финальный счет Анны:»,AnnaScore,»\n»)

else

print(«Анна выиграла игру в кости. Финальный счет Анны:»,AnnaScore,»Финальный счет Алекса:»,AlexScore,»\n»)

Вывод:

Shell

Игра в кости использует модуль random

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 5 Финальный счет Алекса: 2

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 2

Алекс выиграл жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 8

1
2
3
4
5
6
7
8
9
10

Игравкостииспользуетмодульrandom

Аннавыигралажеребьевку.

Аннавыигралаигрувкости.ФинальныйсчетАнны5ФинальныйсчетАлекса2

Аннавыигралажеребьевку.

Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса2

Алексвыигралжеребьевку.

Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса8

Вот и все. Оставить комментарии можете в секции ниже.

Функция экспоненты exp() в Python

Библиотека Math в Python поставляется с функцией , которую можно использовать для вычисления значения . К примеру, — экспонента от . Значение равно .

Метод может быть использован со следующим синтаксисом:

Python

math.exp(x)

1	math.exp(x)

Параметр может быть положительным или отрицательным числом. Если не число, метод возвращает ошибку. Рассмотрим пример использования данного метода:

Python

import math

# Инициализация значений
an_int = 6
a_neg_int = -8
a_float = 2.00

# Передача значений методу exp() и вывод
print(math.exp(an_int))
print(math.exp(a_neg_int))
print(math.exp(a_float))

1
2
3
4
5
6
7
8
9
10
11

importmath

# Инициализация значений

an_int=6

a_neg_int=-8

a_float=2.00

# Передача значений методу exp() и вывод

print(math.exp(an_int))

print(math.exp(a_neg_int))

print(math.exp(a_float))

Вывод

Shell

403.4287934927351
0.00033546262790251185
7.38905609893065

1
2
3

403.4287934927351
0.00033546262790251185
7.38905609893065

Мы объявили три переменные и присвоили им значения с различными числовыми типами данных. Мы передали значения методу для вычисления их экспоненты.

Мы также можем применить данный метод для встроенных констант, что продемонстрировано ниже:

Python

import math

print(math.exp(math.e))
print(math.exp(math.pi))

1
2
3
4

importmath

print(math.exp(math.e))

print(math.exp(math.pi))

Вывод

Shell

15.154262241479262
23.140692632779267

1 2	15.154262241479262 23.140692632779267

При передаче не числового значения методу будет сгенерирована , как показано далее:

Python

import math

print(math.exp(«20»))

1
2
3

importmath

print(math.exp(«20»))

Вывод

Shell

Traceback (most recent call last):
File «C:/Users/admin/mathe.py», line 3, in <module>
print (math.exp(«20»))
TypeError: a float is required

1
2
3
4

Traceback(most recent call last)

File»C:/Users/admin/mathe.py»,line3,in<module>

print(math.exp(«20»))

TypeErrorafloatisrequired

Как видно из примера выше, генерируется ошибка .

Вычисление квадратного корня в Python с помощью модуля cmath

Модуль cmath используется для вычисления квадратного корня в python из Действительного или сложного числа.

Вышеприведенные два метода прекрасно работают для всех положительных вещественных чисел. Но для отрицательных или комплексных чисел это можно сделать следующим образом.

<Пример: Вычисление квадратного корня из числа с помощью math

Выход:

В этой программе мы используем функцию sqrt() в href=”https://docs.python.org/2/library/cmath.html”>cmath (комплексная математика) модуль

Обратите внимание, что мы также использовали функцию eval() вместо float() для преобразования комплексного числа. Кроме того, обратите внимание на то, как форматируются выходные данные. href=”https://docs.python.org/2/library/cmath.html”>cmath (комплексная математика) модуль

href=”https://docs.python.org/2/library/cmath.html”>cmath (комплексная математика) модуль

Комбинации элементов между собой

В библиотеке есть еще одна функция, связанная с перестановками и комбинациями, называемая . Эта функция является разновидностью функции , с той небольшой разницей, что она включает комбинации элементов между собой.

import itertools

values = 

com = itertools.combinations_with_replacement(values, 2)

for val in com:
	print(*val)

Выход:

Мы можем видеть четкое отличие вышеприведенного вывода от вывода с теми же параметрами при передаче в функцию .

Есть комбинации чисел, как будто их несколько экземпляров в списке. В основном это происходит потому, что, когда мы выбираем элемент из списка, вышеуказанная функция снова помещает то же значение, чтобы получить комбинации.

Еще пример. Наша задача — отобразить перестановку заданной строки. Здесь решаем эту проблему в python, используя перестановки встроенных функций (итерируемые).

Input : string = 'XYZ'
Output : XYZ
         XZY 
         YXZ
         YZX
         ZXY       
         ZYX

Алгоритм

Step 1: given string.
Step 2: Get all permutations of string.
Step 3: print all permutations.

Пример кода

from itertools import permutations 
def allPermutations(str1): 
   # Get all permutations of string 'ABC' 
   per = permutations(str1) 
   # print all permutations
   print("Permutation Of this String ::>")
   for i in list(per): 
      print (''.join(i)) 
# Driver program 
if __name__ == "__main__": 
   str1 = input("Enter the string ::>")
   allPermutations(str1)

Вывод

Enter the string ::> abc
Permutation Of this String ::>
abc
acb
bac
bca
cab
cba

Фаза (аргумент) сложного числа

Мы можем представлять комплексное число в качестве вектора, состоящего из двух компонентов в плоскости, состоящей из и оси. Следовательно, два компонента вектора – это реальная часть, и это воображаемая часть.

Угол между вектором и реальной осью определяется как или сложного числа.

Он формально определяется как:

Фаза (номер) (imaginable_part/real_part)

Там, где функция Arctan – это обратная математическая функция.

В Python мы можем получить фазу сложного числа, используя Модуль для сложных чисел. Мы также можем использовать Функция и получить фазу из математического определения.

import cmath
import math

num = 4 + 3j

# Using cmath module
p = cmath.phase(num)
print('cmath Module:', p)

# Using math module
p = math.atan(num.imag/num.real)
print('Math Module:', p)

Выход :

cmath Module: 0.6435011087932844
Math Module: 0.6435011087932844

Обратите внимание, что эта функция возвращает угол фазы в Так что, если нам нужно преобразовать в , мы можем использовать другую библиотеку, как Отказ

import cmath
import numpy as np

num = 4 + 3j

# Using cmath module
p = cmath.phase(num)
print('cmath Module in Radians:', p)
print('Phase in Degrees:', np.degrees(p))

Выход :

cmath Module in Radians: 0.6435011087932844
Phase in Degrees: 36.86989764584402

Звук

Благодаря нескольким очень полезным
модулям работать со звуком в Python довольно
просто.

pySonic. Python-враппер для высокопроизводительной кроссплатформенной звуковой библиотеки FMOD.

PyMedia. Модуль Python для манипуляций с файлами WAV, MP3, Ogg, AVI, DivX, DVD, CD-DA и др. Позволяет анализировать, демультиплексировать и мультиплексировать, декодировать и кодировать все поддерживаемые форматы. Может компилироваться для Windows, Linux и Cygwin.

PMIDI. Библиотека PMIDI служит оберткой для библиотеки Windows MIDI Streams, обеспечивая возможность использования последней в Python. Благодаря PMIDI разработчики могут на лету генерировать в своем коде синтезированные музыкальные последовательности, чтобы они проигрывались для пользователей.

Mutagen. Модуль для обработки метаданных аудио. Поддерживает аудиофайлы FLAC, M4A, Musepack, MP3, Ogg FLAC, Ogg Speex, Ogg Theora, Ogg Vorbis, True Audio и WavPack.

Тригонометрические функции

Тригонометрические функции для комплексного номера также доступны в модуль.

import cmath

a = 3 + 4j

print('Sine:', cmath.sin(a))
print('Cosine:', cmath.cos(a))
print('Tangent:', cmath.tan(a))

print('ArcSin:', cmath.asin(a))
print('ArcCosine:', cmath.acos(a))
print('ArcTan:', cmath.atan(a))

Выход :

Sine: (3.853738037919377-27.016813258003936j)
Cosine: (-27.034945603074224-3.8511533348117775j)
Tangent: (-0.0001873462046294784+0.999355987381473j)
ArcSin: (0.6339838656391766+2.305509031243477j)
ArcCosine: (0.9368124611557198-2.305509031243477j)
ArcTan: (1.4483069952314644+0.15899719167999918j)

Заключение

Итак, в 4-х рассмотренных нами категориях были представлены модули, которые должен знать каждый разработчик Python. Этот язык программирования предоставляет удивительные возможности, однако необязательно использовать все из них. В зависимости от решаемых задач какие-то подойдут лучше других. Вы никогда не ошибетесь, если будете выбирать инструмент согласно своим целям.

5 доказательств силы итерируемых объектов в Python
К подготовке и публикации первого пакета Python готовы!
4 шага к совершенству: правила для идеальных функций

Читайте нас в Telegram, VK и

Перевод статьи Samuel Martins: Most Useful Modules Every Python Developer Should Know

Десятичный модуль(decimal) python

Преобразование числовых типов

Преобразование целых чисел в числа с плавающей запятой

Преобразование чисел с плавающей запятой в ​​целые числа

Преобразование чисел путем деления

Гиперболические функции

Игра в кости с использованием модуля random в Python

Графический интерфейс

Практическая работа. Создание собственного модуля

Тригонометрические функции в Python

Классификационные функции

Фаза комплексного числа

Математические методы

Игра в кости с использованием модуля random в Python

Функция экспоненты exp() в Python

Вычисление квадратного корня в Python с помощью модуля cmath

Комбинации элементов между собой

Фаза (аргумент) сложного числа

Звук

Тригонометрические функции

Заключение

Преобразование чисел с плавающей запятой в целые числа